(1)证明:∵点O、O′关于直线y=x+b的对称,
∴直线y=x+b是线段OO′的垂直平分线,∴AO=AO′,BO=BO′。
又∵OA,OB是⊙O的半径,∴OA=OB。
∴AO=AO′=BO=BO′。∴四边形OAO′B是菱形.
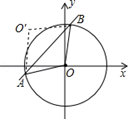
(2)解:如图,设直线y=x+b与x轴、y轴的交点坐标分别是

N(-b,0),P(0,b),AB与OO′相交于点M。
则△ONP为等腰直角三角形,∴∠OPN=45°。
∵四边形OAO′B是菱形,∴OM⊥PN。
∴△OMP为等腰直角三角形。
当点O′落在圆上时,OM=
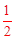
OO′=1。
在Rt△OMP中,由勾股定理得:OP=
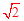
,即b=
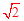
。


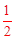 OO′=1。
OO′=1。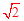 ,即b=
,即b=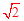 。
。
