
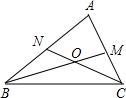
 如图,△ABC的角平分线BM,CN相交于O.
如图,△ABC的角平分线BM,CN相交于O. 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
 23、如图,BD是∠ABC的平分线,ED∥BC,∠4=∠3,则EF也是∠AED的平分线.
23、如图,BD是∠ABC的平分线,ED∥BC,∠4=∠3,则EF也是∠AED的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
 16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是
16、如图,在△ABC中,AD是△ABC中∠CAB的角平分钱,要使△ADC≌△ADE,需要添加一个条件,这个条件是查看答案和解析>>
科目:初中数学 来源: 题型:044
如图,△ABC沿射线BC的方向平移一定距离后成为△DEF.
(1)找出图中由于平称而产生的相等的线段,并指出图中的对应线段及对应角;
(2)你能从对应角相等找出图中互相平行的线段吗?说说你的做法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com