
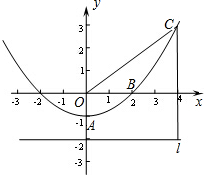
 如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).
如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).分析 (1)将点A、B的坐标代入解析式,求出a、c的值即可得出解析式;
(2)分别求出圆的半径和抛物线上的点到y=-2的长度,继而可判断圆与直线l的位置关系;
(3)根据(2)求出的结果可得,抛物线上任意一点P与它到直线y=-2的距离都相等,因此只要在直线y=-2上找到一点Q使∠OQA=30°,就能作出等边三角形OPQ,据此找出满足条件的坐标.
解答 解:(1)将点A、B的坐标代入抛物线y=ax2+c得,
$\left\{\begin{array}{l}{c=-1}\\{a=\frac{1}{4}}\end{array}\right.$,
则抛物线的解析式为:y=$\frac{1}{4}$x2-1;
(2)设点C坐标为(x,y),
则OC=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{x}^{2}+\frac{{x}^{4}}{16}-\frac{{x}^{2}}{2}+1}$=$\frac{1}{4}$x2+1,
∵点C到直线l的距离为:$\frac{1}{4}$x2-1+2=$\frac{1}{4}$x2+1=OC,
∴圆的半径=点C到直线l的距离,
∴圆C与直线l相切;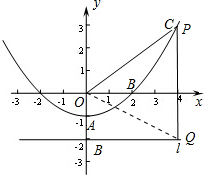
(3)由(2)得,抛物线上任意一点P与它到直线y=-2的距离都相等,
∴当∠PQO=60°时,△OPQ为等边三角形,
即当∠OQA=30°时,△OPQ为等边三角形,
∵OB=2,∠OQB=30°,
∴BQ=2$\sqrt{3}$,
点Q坐标为(2$\sqrt{3}$,-2),
同理可得,当点P在第二象限,点Q在第三象限时,此种情况仍然成立,
此时点Q坐标为(-2$\sqrt{3}$,-2),
综上所述,满足条件的P点坐标为(2$\sqrt{3}$,2),(-2$\sqrt{3}$,2).
点评 本题考查了二次函数的综合应用,涉及了待定系数法求函数解析式、圆与直线的位置关系、等边三角形的性质等知识点,综合性较强,难度较大,解答本题的关键是要会利用数形结合的思想把代数和几何图形结合起来,进而解决问题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com