
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为BC中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连接CF、AF、AD,AD与CF交于点G.
(1)求证:△ACD≌△CBF;
(2)AD与CF的关系是 ;
(3)求证:△ACF是等腰三角形;
(4)△ACF可能是等边三角形吗? (填“可能”或“不可能”).
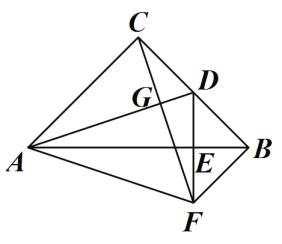
【答案】(1)见解析;(2)AD=CF,且AD⊥CF;(3)见解析;(4)不可能
【解析】
(1)∠CAB=∠CBA=![]() ,且BF∥AC,则∠FBE=∠CAB=
,且BF∥AC,则∠FBE=∠CAB=![]() ,则∠DBF=
,则∠DBF=![]() ,又DE⊥AB,则∠BDE=
,又DE⊥AB,则∠BDE=![]() ,则△BDF为等腰直角三角形,∴DB=BF,又D为BC中点,所以CD=BF.即可证明△ACD≌△CBF.
,则△BDF为等腰直角三角形,∴DB=BF,又D为BC中点,所以CD=BF.即可证明△ACD≌△CBF.
(2)由△ACD≌△CBF可判断,AD=CF,又∠CAD=∠BCF,则∠CGD=![]() ,所以AD⊥CF.
,所以AD⊥CF.
(3)由(1)知AB垂直平分DF,由三线合一知△ADF是等腰三角形,则AD=AF,由(2)知AD=CF,所以AF=CF,即可证明.
(4)在Rt△ACD中易知,AD>AC,又AD=AF=CF,所以△ACF不可能是等边三角形.
(1)证明:∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°,
∵BF∥AC,
∴∠FBE=∠CAB=45°,
∴∠CBF=90°,又DE⊥AB,
∴∠FDB=45°,
∴∠DFB=45°,
∴BD=BF,又D为BC中点,
∴CD=BF,
在△ACD和△CBF中,
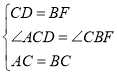 ,
,
∴△ACD≌△CBF;
(2)∵△ACD≌△CBF,
∴AD=CF,∠CAD=∠BCF
∴∠CAD+∠CDA=∠BCF+∠CDA=![]()
∴AD⊥CF
故答案为:AD=CF且AD⊥CF;
(3)由(2)知
∵DF⊥AE,DE=EF,
由三线合一可知,△ADF是等腰三角形
∴AD=AF,
∵AD=CF,
∴AF=CF,
∴△ACF是等腰三角形;
(4)在Rt△ACF中,AC<AD,
由(2)知,AD=AF
∴AC<AF,
∴△ACF不可能是等边三角形,
故答案为:不可能.


科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b与反比例函数![]() 的图象交于A(﹣1,m)、B(n,﹣1)两点.
的图象交于A(﹣1,m)、B(n,﹣1)两点.
(1)求出A、B两点的坐标;
(2)求出这个一次函数的表达式;
(3)根据图象,写出使一次函数值大于反比例函数值的x的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
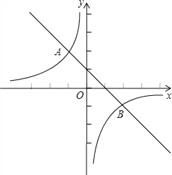
【题目】在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
(1)现将△ABC先向左平移5个单位长度,再向上平移2个单位长度,得到△A1B1C1,请在平面直角坐标系中画出△A1B1C1.
(2)此时平移的距离是 ;
(3)在平面直角坐标系中画出△ABC关于点O成中心对称的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生自主意识,拓宽学生视野,促进学习与生活的深度融合我市某中学决定组织部分学生去青少年综合实践基地进行综合实践活动在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生现有甲、乙两种大客车它们的载客量和租金如表所示
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 42 |
租金(元/辆) | 300 | 400 |
学校计划此实践活动的租车总费用不超过3100元,为了安全每辆客车上至少要有2名老师.
(1)参加此次综合实践活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,租用客车总数为多少辆?
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元,已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次采购的数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.为出口需要,所有采购的大蒜必须在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半.为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8cm,BC=6cm.点E是CD边上的一点,且DE=2cm,动点P从A点出发,以2cm/s的速度沿A→B→C→E运动,最终到达点E.当△APE的面积等于20cm2时,则点P运动的时间为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请在横线上填上合适的内容,完成下面的证明:
如图,射线AH交折线ACGFEN于点B、D、E.已知∠A=∠1,∠C=∠F,BM平分∠CBD,EN平分∠FEH.求证:∠2=∠3.

证明:∵∠A=∠1(已知)
∴AC∥GF( )
∴( )( )
∵∠C=∠F(已知)
∴∠F=∠G
∴( )( )
∴( )( )
∵BM平分∠CBD,EN平分∠FEH
∴∠2= ∠3=
∴∠2=∠3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com