Question

已知：⊙O的半径为3cm，点P和圆心O的距离为6cm，经过点P和⊙O的两条切线，求这两条切线的夹角及切线长．

Answer 1

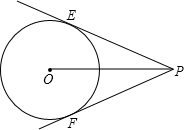
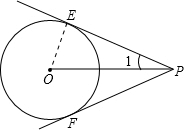
解：连接OE，则OE⊥PE，由切线长定理可知：PE=PF，∠EPF=2∠1，在Rt△POE中，OP=6，OE=3，
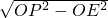
∴PE===3cm，
sin∠1===，
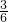
∴∠1=30°，
∴∠EPF=2∠1=60°．
故这两条切线的夹角为60°，切线长为3cm．
分析：根据切线长定理：从圆外一点到圆的两条切线的长相等，那点与圆心的连线平分切线的夹角，可知PE=PF，∠EPF=2∠1；
由切线的性质知：OE⊥PE，故在Rt△PEO中，根据勾股定理可得PE的长，求出sin∠1=的值可知∠1，根据∠EPF=2∠1可求出两条切线的夹角．
点评：本题综合考查了切线的性质和解直角三角形的运算方法．