
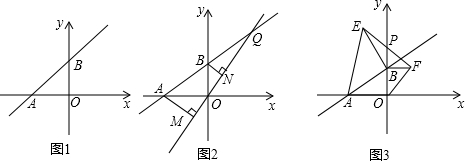
���� ��1����y=0����y=mx+5m�����x��ֵ�������õ�A�����ꣻ
��2����Rt��BON�У����ù��ɶ������ON=$\sqrt{O{B}^{2}-B{N}^{2}}$=4���ٸ���AAS�õ���AMO�ա�ONB���ö�Ӧ�߶�����ȣ�
��3����ͼ����EK��y����K�㣬����AAS�õ���AOB�ա�BKE������ȫ�������ζ�Ӧ����ȵõ�OA=BK��EK=OB��������AAS�õ���PBF�ա�PKE��Ѱ������߶Σ�������ת������PB�ij���
��� �⣺��1����ֱ��l��y=mx+5m��
�൱y=0ʱ��mx+5m=0��
��A��-5��0����
��2����Rt��BON�У��ߡ�ONB=90�㣬OB=OA=5��BN=3��
��ON=$\sqrt{O{B}^{2}-B{N}^{2}}$=4��
�ڡ�AMO���ONB�У�
$\left\{\begin{array}{l}{��OAM=��BON}\\{��AMO=��BNO}\\{OA=OB}\end{array}\right.$��
���AMO�ա�ONB��AAS����
��AM=ON=4��OM=BN=3��
��MN=OM+ON=3+4=7��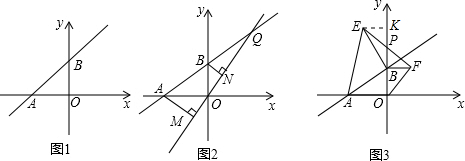 ��3����ͼ����EK��y����K�㣬
��3����ͼ����EK��y����K�㣬
�ߡ�ABEΪ����ֱ�������Σ�
��AB=BE����ABE=90�㣬
���EBK+��ABO=90�㣬
�ߡ�EBK+��BEK=90�㣬
���ABO=��BEK��
�ڡ�AOB�͡�BKE�У�
$\left\{\begin{array}{l}{��AOB=��BKE=90��}\\{��ABO=��BEK}\\{AB=BE}\end{array}\right.$��
���AOB�ա�BKE��AAS����
��OA=BK��OB=EK��
�ߡ�OBFΪ����ֱ�������Σ�
��OB=BF��
��EK=BF��
�ڡ�EKP�͡�FBP�У�
$\left\{\begin{array}{l}{��EKP=��FBP=90��}\\{��KPE=��BPF}\\{EK=FB}\end{array}\right.$��
���PKE�ա�PBF��AAS����
��PK=PB��
��PB=$\frac{1}{2}$BK=$\frac{1}{2}$OA=$\frac{5}{2}$��
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У�ȫ�������ε��ж������ʣ�����ֱ�������ε����ʣ����ɶ�����һ�κ�����������Ľ��㣬��������ȫ�������ε��ж��������ǽⱾ��Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
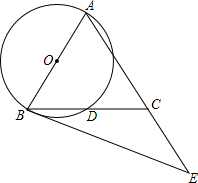 ��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ڵ�D����E��AC���ӳ����ϣ��ҡ�CBE=$\frac{1}{2}$��BAC��
��ͼ���ڡ�ABC�У�AB=AC����ABΪֱ���ġ�O��BC�ڵ�D����E��AC���ӳ����ϣ��ҡ�CBE=$\frac{1}{2}$��BAC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
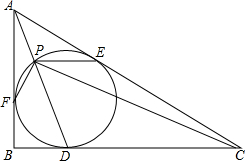 ��ֱ��������ABC�У���B=90�㣬��������Բ�ֱ����BC��CA��AB�������D��E��F������AD��������Բ�ཻ����һ��P������PC��PE��PF����֪PC��PF����֤��
��ֱ��������ABC�У���B=90�㣬��������Բ�ֱ����BC��CA��AB�������D��E��F������AD��������Բ�ཻ����һ��P������PC��PE��PF����֪PC��PF����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
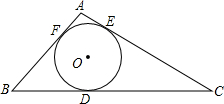 ��֪����ͼ����O�ǡ�ABC������Բ���ֱ���BC��AB��AC�ڵ�D��E��F����ABC���ܳ�Ϊ24cm��BC=10cm����AE=2cm��
��֪����ͼ����O�ǡ�ABC������Բ���ֱ���BC��AB��AC�ڵ�D��E��F����ABC���ܳ�Ϊ24cm��BC=10cm����AE=2cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
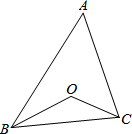 ��ͼ���ڡ�ABC�У���A=50�㣬��O���������ģ����BOC���ڣ�������
��ͼ���ڡ�ABC�У���A=50�㣬��O���������ģ����BOC���ڣ�������| A�� | 125�� | B�� | 115�� | C�� | 105�� | D�� | 95�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com