
 x2+10,并且BD=
x2+10,并且BD= CD.
CD.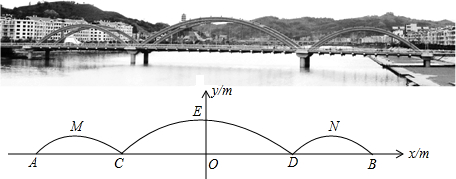
 x2+10,
x2+10, x2+10
x2+10 x2+10,
x2+10, CD,
CD,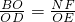 ,
,
 ,
,
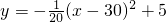 .
.

科目:初中数学 来源: 题型:
| 1 |
| 40 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏昆山兵希中学九年级上学期第一次阶段测试数学试卷(解析版) 题型:解答题
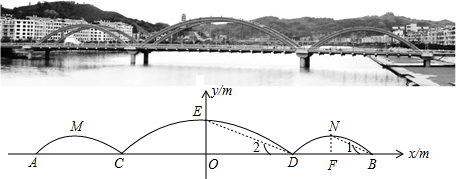
许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称.经过测算,中间抛物线的解析式为:y=- x2+10,并且BD=
x2+10,并且BD= CD.
CD.

(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
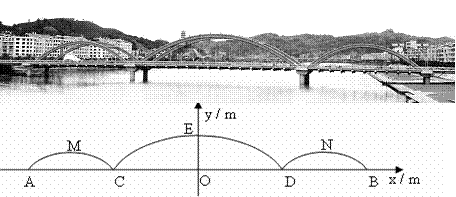
许多桥梁都采用抛物线型设计,小明将他家乡的彩虹桥按比例缩小后,绘成如下的示意图,图中的三条抛物线分别表示桥上的三条钢梁,x轴表示桥面,y轴经过中间抛物线的最高点,左右两条抛物线关于y轴对称。经过测算,中间抛物线的解析式为
y=-![]() x2+10,并且BD=
x2+10,并且BD=![]() CD。
CD。
(1)求钢梁最高点离桥面的高度OE的长;
(2)求桥上三条钢梁的总跨度AB的长;
(3)若拉杆DE∥拉杆BN,求右侧抛物线的解析式。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com