
 已知a、b、c在数轴上的位置如图所示:
已知a、b、c在数轴上的位置如图所示:分析 (1)根据绝对值的性质,可化简绝对值,根据分式的性质,可化简分式,根据分式的加减,可得答案;
(2)根据有理数的加减法,可确定和的大小,根据有理数的大小比较,可得答案.
解答 解:(1)由数轴,得
a<c<0<b,且|a|>|c|>|b|,
$\frac{a}{|ab|}$+$\frac{1}{|b|}$-$\frac{2bc}{|bc|}$=-$\frac{a}{ab}$+$\frac{1}{b}$+$\frac{2bc}{bc}$=2;
(2)a<a+b<0,b-c>0,a+c<a,
a+c<a+b<b-c.
点评 本题考查了有理数大小比较,利用有理数的加法得出a<a+b<0,a+c<a是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
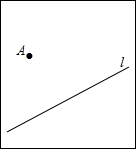 点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:
点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com