

解:(1)如图: |
|
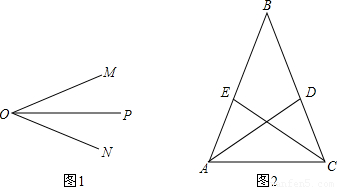
| (2)FE与F之间的数量关系为FE=FD 如图,在AC上截取AG=AE,连接FG 由(1)知∠EAF=∠GAF, 又∵AF为公共边, ∴△EAF≌△GAF, ∴FE=FG,∠EFA=∠GFA=60° ∴∠GFC=180°-60°-60°=60° 又∵∠DFC=∠EFA=60°, ∴∠DFC=∠GFC 由(1)知∠DCF=∠GCF, 又∵CF为公共边, ∴△FDC≌△FGC, ∴FD=FG ∴FE=FD |
 |
| (3)(2)中的结论FE=FD仍然成立,理由如下: 在AC上截取AG=AE,连接FG,因为∠1=∠2,AF为公共边,可证△AEF≌△AGF, 所以∠AFE=∠AFG,FE=FG, 由∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线, 可得∠2+∠3=60°, 所以∠AFE=∠CFD=∠AFG=60°, 所以∠CFG=180°-∠2-∠3-∠AFG=60°, 由∠3=∠4及FC为公共边, 可得△CFG≌△CFD, 所以FG=FD, 所以FE=FD。 |
 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
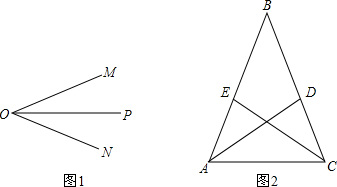
 25、如图1,OP是∠MON的平分线,请你在该图形上利用尺规作出一对以OP所在直线为对称轴的全等三角形.
25、如图1,OP是∠MON的平分线,请你在该图形上利用尺规作出一对以OP所在直线为对称轴的全等三角形.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:四川省期末题 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年江苏省泰州市兴化市板桥初级中学初三数学练习卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com