练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形EFGH四个顶点分别在菱形ABCD的四条边上，BE=BF，将△AEH，△CFG分别沿边EH，FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的 时，则 为（ ）

    A.
    B.2
    C.
    D.4

    【答案】A
    【解析】解：依题可得阴影部分是菱形.
    ∴设S菱形ABCD=16,BE=x.
    ∴AB=4.
    ∴阴影部分边长为4-2x.
    ∴（4-2x）2=1.
    ∴4-2x=1或4-2x=-1.
    ∴x=或x=（舍去）.
    ∴==.
    所以答案是A.
    【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，函数 y=2x 与 y=ax+5 的图象相交于点 A（m，4）．

    （1）求 A 点坐标及一次函数 y=ax+5 的解析式；

    （2）设直线 y=ax+5 与 x 轴交于点 B，求△AOB 的面积；

    （3）求不等式 2x＜ax+5 的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，AB=AC.

    （1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=_____度；

    （2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=_______度；

    （3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：____________________.

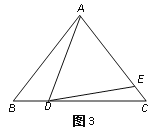
    （4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读对人成长的影响是巨大的，一本好书往往能改变人的一生．如图是某校三个年级学生人数分布的扇形统计图，其中八年级人数为408人，下表是该校学生阅读课外书籍情况统计表．根据图表中的信息，可知该校学生平均每人阅读课外书________本．

    图书种类

    频数

    频率

    科普知识

    840

    B

    名人传记

    816

    0.34

    漫画丛记

    A

    0.25

    其他

    144

    0.06

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和反射出的光线与平面镜所夹的角相等.

    （1）如图，一束光线m射到平面镜a上，被a反射到平面镜b上，又被b镜反射出去，若b镜反射出的光线n平行于m，且∠1=30，则∠2= ，∠3= ；

    （2）在（1）中，若∠1=70，则∠3= ；若∠1=a，则∠3= ；

    （3）由（1）（2）请你猜想：当∠3= 时，任何射到平面镜a上的光线m经过平面镜a和b的两次反射后，入射光线m与反射光线n总是平行的？请说明理由.

    （提示：三角形的内角和等于180）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】建立模型：

    如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．

    操作：

    过点A作AD⊥l于点D，过点B作BE⊥l于点E．求证：△CAD≌△BCE．

    模型应用：

    （1）如图2，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．

    （2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

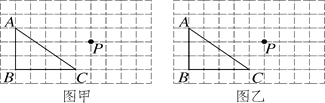
    【题目】如图，在方格纸中，每个小方格的边长均为1个长度单位，三角形ABC的三个顶点和点P都在小方格的顶点上．要求：①将三角形ABC平移，使点P落在平移后的三角形内部；②平移后的三角形的顶点在方格的顶点上．请你在图甲和图乙中分别画出符合要求的一个示意图，并写出平移的方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察下列各式

    （x﹣1）（x+1）＝x2﹣1

    （x﹣1）（x2+x+1）＝x3﹣1

    （x﹣1）（x3+x2+x+1）＝x4﹣1

    （1）根据以上规律，则（x﹣1）（x6+x5+x4+x3+x2+x+1）＝　 　；

    （2）你能否由此归纳出一般规律（x﹣1）（xn+xn﹣1+……+x+1）＝　 　；

    （3）根据以上规律求32018+32017+32016+…32+3+1的结果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y＝（m＋1）x2－|m|＋n＋4．

    （1）当m，n为何值时，此函数是一次函数？

    （2）当m，n为何值时，此函数是正比例函数？

    查看答案和解析>>

    同步练习册答案