解:(1)线段EF与AF、BE的关系为:EF
2=AF
2+BE
2.理由如下:
延长ED至DG,使DG=DE,连接AG,FG,如图1,
∵FD⊥GN,
∴FG=EF.
∵D是AB中点,
∴AD=BD,
∵∠ADG=∠EDB,
∴△BED≌△AGD,
∴AG=BE,∠GAD=∠B.
∵△ABC是直角三角形,
∴∠BAC+∠B=90°,
∴∠BAC+∠DAG=90°,
∴AG
2+AF
2=FG
2.
∴EF
2=AF
2+BE
2.
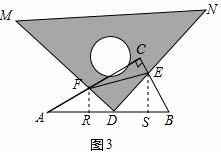
(2)作FR⊥AB,ES⊥AB,(如图3)
∴∠FRA=∠ESB=90°.
∵∠A=30°,
∴∠B=60°,
∴∠SEB=30°,
∴SB=

BE,SE=

SB.
∵在Rt△FCE中,由勾股定理,得,CF
2+CE
2=EF
2,
∵EF
2=AF
2+BE
2,
∴CF
2+CE
2=AF
2+BE
2,
∵∠A=30°,BC=2,
∴AB=4,AC=2

,
∴CF=2

-x,CE=2-BE.
∴(2

-x)
2+(2-BE)
2=x
2+BE
2
∴BE=4-

x,
∴SB=2-
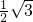
x,
∴SE=2

-

x,
∴y=

×2×2

-2×

x•

-

×2×(2

-

x),
y=2

-

x-2

+

x,
y=x
当E点与C点重合时,ED=CD=2,DF=

,则CF=
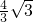
,
∴x=

;
当E点与B点重合时,AF=
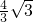
,
∴x的取值范围为:


≤x≤


(3)作AP⊥MD,(如图2)
∴AP=

,
∵CD=2,
∴DE=2

,EC=4,
∴S
△AHC+
S△CHE=S
△AEC.
∴

×

CH+

×CH×2

=

×4×2

,
∴CH=

,
∴DH=

-2=

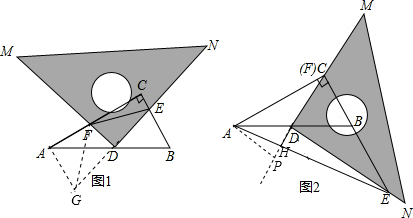
分析:(1)延长ED至DG,使DG=DE,连接AG,FG,证明△BED≌△AGD,可以得出∠GAD=∠B,AG=BE,由∠BAC+∠B=90°,得出∠GAF=90°,得出△GAF是直角三角形,∵MD⊥DN,GD=DE,得出FG=EF,由勾股定理就可以得出AG
2+AF
2=FG
2,从而得出结论.
(2)作FR⊥AB,ES⊥AB分别于R、S,在Rt△ARF中由勾股定理可以表示出FR,从而可以表示出△FAD的面积,由勾股定理,得CF
2+CE
2=EF
2,再由(1)的结论建立等量关系表示出BE,从而求出ES,就可以表示出△EDB的面积,进而可以表示出y的值.
(3)作AP⊥MD,交MD的延长线于点P,由条件可以求出AP=

,DE=2

,EC=4,可以求出△ACE的面积,然后用S
△AHC+
S△CHE=S
△AEC建立等量关系可以求出CH的值,再减去CD的值就求出了DH.
点评:本题考查了等腰直角三角形的性质,全等三角形的判定与性质,勾股定理的运用,含30°的直角三角形的性质.

 BE,SE=
BE,SE= SB.
SB. ,
, -x,CE=2-BE.
-x,CE=2-BE. -x)2+(2-BE)2=x2+BE2
-x)2+(2-BE)2=x2+BE2 x,
x, x,
x, -
- x,
x, ×2×2
×2×2 -2×
-2× x•
x• -
- ×2×(2
×2×(2 -
- x),
x), -
- x-2
x-2 +
+ x,
x, ,则CF=
,则CF= ,
, ;
;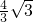 ,
,
 ≤x≤
≤x≤


 ,
, ,EC=4,
,EC=4, ×
× CH+
CH+ ×CH×2
×CH×2 =
= ×4×2
×4×2 ,
, ,
, -2=
-2=

 ,DE=2
,DE=2 ,EC=4,可以求出△ACE的面积,然后用S△AHC+S△CHE=S△AEC建立等量关系可以求出CH的值,再减去CD的值就求出了DH.
,EC=4,可以求出△ACE的面积,然后用S△AHC+S△CHE=S△AEC建立等量关系可以求出CH的值,再减去CD的值就求出了DH.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为