
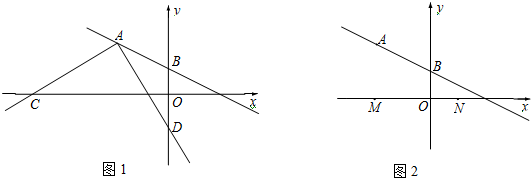
���� ��1����ֱ��AB����ʽΪy=kx+b����A��B��������г������飬���������Ľ�õ�k��b��ֵ������ȷ����ֱ��AB����ʽ��
��2������CAD���ŵ�A��תʱ��OC-OD��ֵ���䣬����Ϊ����A��AE��ֱ��x�ᣬAF��ֱ��y�ᣬ����ͬ�ǵ������ȵõ�һ�Խ���ȣ����A������õ�AE=AF��������ֱ֪����ȣ�����ASA�õ�������AEC��������AFDȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�EC=FD���������OC-OD��ֵ���ɣ�
��3��������������ǣ��ٵ�MΪֱ�Ƕ���ʱ����NΪֱ�Ƕ���ʱ����PΪֱ�Ƕ���ʱ���ֱ����P���꼴�ɣ�
���  �⣺��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�⣺��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�ߵ�A��-4��4������B��0��2����ֱ��AB�ϣ�
��$\left\{\begin{array}{l}{-4k+b=4}\\{b=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��AB�Ľ���ʽΪ��y=-$\frac{1}{2}$x+2��
��2�����䣮�������£�
����A�ֱ���x�ᣬy��Ĵ��ߣ�����ֱ�ΪE��F�����ͼ�����ɵá�AEC=��AFD=90�㣬
�֡ߡ�BOC=90�㣬
���EAF=90�㣬����DAE+��DAF=90�㣬
�ߡ�CAD=90�㣬����DAE+��CAE=90�㣬
���CAE=��DAF��
��A��-4��4����
��OE=AF=AE=OF=4��
�ڡ�AEC�͡�AFD�У�
$\left\{\begin{array}{l}{��CAE=��DAF}\\{AE=AF}\\{��AEC=��AFD=90��}\end{array}\right.$��
���AEC�ա�AFD��ASA����
��EC=FD��
��OC-OD=��OE+EC��-��FD-OF��=OE+OF=8��
��OC-OD��ֵ�������仯��ֵΪ8��
��3���ٵ�MΪֱ�Ƕ���ʱ����P�ĺ�����Ϊ-4��
�ߵ�P��ֱ��AB�ϣ�
��x=-4����y=-$\frac{1}{2}$x+2�ã�y=4��
���P������ΪP��-4��4����
�ڵ�NΪֱ�Ƕ���ʱ����P�ĺ�����Ϊ2��
�ߵ�P��ֱ��AB�ϣ�
��x=2����y=-$\frac{1}{2}$x+2�ã�y=1��
���P������ΪP��2��1����
�۵�PΪֱ�Ƕ���ʱ��
�ߵ�P��ֱ��AB�ϣ������P������Ϊ��x��-$\frac{1}{2}$x+2����
��MP2=��x+4��2+��-$\frac{1}{2}$x+2��2��NP2=��x-2��2+��-$\frac{1}{2}$x+2��2��
��Rt��PMN��MP2+NP2=MN2��MN=6��
�ࣨx+4��2+��-$\frac{1}{2}$x+2��2+��x-2��2+��-$\frac{1}{2}$x+2��2=62��
��ã�x1=-$\frac{4\sqrt{5}}{5}$��x2=$\frac{4\sqrt{5}}{5}$��
��P��-$\frac{4\sqrt{5}}{5}$��$\frac{2\sqrt{5}}{5}$+2����$\frac{4\sqrt{5}}{5}$��-$\frac{2\sqrt{5}}{5}$+2����
�����������������������е�P������Ϊ��-4��4����2��1����-$\frac{4\sqrt{5}}{5}$��$\frac{2\sqrt{5}}{5}$+2����$\frac{4\sqrt{5}}{5}$��-$\frac{2\sqrt{5}}{5}$+2����
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У�����ϵ������һ�κ�������ʽ��������ͼ�����ʣ�ȫ�������ε��ж������ʣ����ɶ����������˷������۵�˼�룬�����������ʼ������ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 3 | C�� | -2 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���BAC=120�㣬AB=AC��AD��BC������ΪD�����BAD�Ķ�����60�㣮
��ͼ����ABC�У���BAC=120�㣬AB=AC��AD��BC������ΪD�����BAD�Ķ�����60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
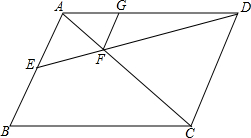 ��ͼ��?ABCD�У�AB=6��EΪAB�е㣬DE��AC�ڵ�F��FG��AB��AD�ڵ�G�����߶�FG�ij���
��ͼ��?ABCD�У�AB=6��EΪAB�е㣬DE��AC�ڵ�F��FG��AB��AD�ڵ�G�����߶�FG�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��һ��һ����Ϊ30�㣬��С�䳤Ϊ4��ֱ��������ֽƬ����ͼ����ʾ����λ������������ƴ��һ���ı��Σ������ı��ε��ܳ���8+4$\sqrt{3}$��16��
��һ��һ����Ϊ30�㣬��С�䳤Ϊ4��ֱ��������ֽƬ����ͼ����ʾ����λ������������ƴ��һ���ı��Σ������ı��ε��ܳ���8+4$\sqrt{3}$��16���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com