练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
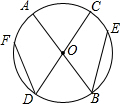
    19．如图，AB，CD是⊙O的直径，DF，BE是弦，且DF=BE，求证：$\widehat{AF}$=$\widehat{CE}$．

    分析 根据圆心角、弧、弦的关系定理得到$\widehat{DF}$=$\widehat{BE}$，证明即可．

    解答 证明：∵DF=BE，
    ∴$\widehat{DF}$=$\widehat{BE}$，
    ∴$\widehat{DC}$-$\widehat{DF}$=$\widehat{AB}$-$\widehat{BE}$，即$\widehat{FC}$=$\widehat{EA}$，
    ∴$\widehat{FC}$-$\widehat{AC}$=$\widehat{EA}$-$\widehat{AC}$，
    ∴$\widehat{AF}$=$\widehat{CE}$．

    点评 本题考查的是圆心角、弧、弦的关系，掌握在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．某汽车厂原计划上半年每月生产汽车20辆，实际生产量规定超过20辆记为“+”，不足20辆记为“-”，实际每月生产量与计划每月生产量相比情况如下表：
    月份一二三四五六
    增减量/辆+3-2-1+4+2-5
    （1）生产量最多的一个月比生产量最少的一个月多生产多少辆？
    （2）上半年内的实际总生产量是怎么变化的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知多项式A，B，其中B=5x2+3x-4，马小虎同学在计算“3A+B”时，误将“3A+B”看成了“A+3B”，求得的结果为12x2-6x+7．
    （1）求多项式A；
    （2）求出3A+B的正确结果；
    （3）当x=-$\frac{1}{3}$时，求3A+B的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．已知：AB∥CD，∠1=80°，∠2=50°，则∠ADC等于（　　）
    A．110°B．120°C．130°D．140°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

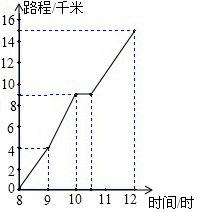    14．如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S（单位：千米）与时间t（单位：时）的变量关系的图象．根据图象回答问题：
    （1）在这个变化过程中，自变量是时间，因变量是路程．
    （2）9时所走的路程是多少？他休息了多长时间？
    （3）他从休息后直至到达目的地这段时间的平均速度是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．求下列各式的值：
    （1）cos260°-sin260°；
    （2）$\frac{co{s}^{2}45°}{si{n}^{2}45°}$-tan45°；
    （3）tan60°-2sin30°•cos30°；
    （4）3tan30°-tan245°-2sin60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．一个二次函数经过点（1，1），它的顶点坐标是（3，5），求这个二次函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．用方程解决问题：
    王老师把一个正方形的边长增加了4cm得到的新正方形的面积比原来正方形的面积增加了64cm2，求原来正方形的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．足球比赛规定：胜一场得3分，平一场得1分，负一场不得分，某队在北京奥运会比赛中结果是胜3场，平2场，负4场，则得分为11分．

    查看答案和解析>>

    同步练习册答案