
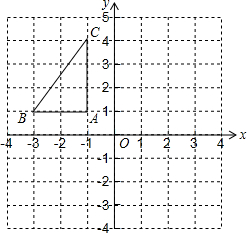 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为科目:初中数学 来源: 题型:解答题
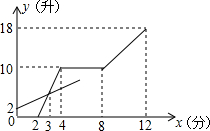 现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
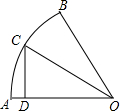 如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$.
如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
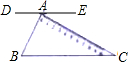 如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )
如图,一块含30°角的直角三角板ABC的直角顶点A在直线DE上,且BC∥DE,则∠CAE等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
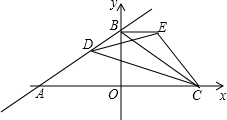 如图,直线y=$\frac{1}{2}$x+2交x轴、y轴于A、B两点,点C与点A关于y轴对称,点D是线段AB上一个动点,ED=EC,且sin∠EDC=$\frac{\sqrt{5}}{5}$.
如图,直线y=$\frac{1}{2}$x+2交x轴、y轴于A、B两点,点C与点A关于y轴对称,点D是线段AB上一个动点,ED=EC,且sin∠EDC=$\frac{\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
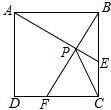 如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,在边长为$\sqrt{3}$的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),在运动过程中,则线段CP的最小值为$\frac{\sqrt{15}-\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
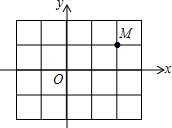 如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )
如图,在平面直角坐标系中,将点M(2,1)向下平移2个单位长度得到点N,则点N的坐标为( )| A. | (2,-1) | B. | (2,3) | C. | (0,1) | D. | (4,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com