
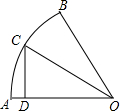
 如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$.
如图,在扇形OAB中,∠AOB=60°,扇形半径为r,点C在$\widehat{AB}$上,CD⊥OA,垂足为D,当△OCD的面积最大时,$\widehat{AC}$的长为$\frac{1}{4}πr$. 分析 由OC=r,点C在$\widehat{AB}$上,CD⊥OA,利用勾股定理可得DC的长,求出OD=$\frac{\sqrt{2}}{2}r$时△OCD的面积最大,∠COA=45°时,利用弧长公示得到答案.
解答 解:∵OC=r,点C在$\widehat{AB}$上,CD⊥OA,
∴DC=$\sqrt{O{C}^{2}-O{D}^{2}}$=$\sqrt{{r}^{2}-O{D}^{2}}$,
∴S△OCD=$\frac{1}{2}$OD•$\sqrt{{r}^{2}-O{D}^{2}}$,
∴S△OCD2=$\frac{1}{4}$OD2•(r2-OD2)=-$\frac{1}{4}$OD4+$\frac{1}{4}$r2OD2=-$\frac{1}{4}$(OD2-$\frac{{r}^{2}}{2}$)2+$\frac{{r}^{4}}{16}$
∴当OD2=$\frac{{r}^{2}}{2}$,即OD=$\frac{\sqrt{2}}{2}$r时△OCD的面积最大,
∴∠OCD=45°,
∴∠COA=45°,
∴$\widehat{AC}$的长为:$\frac{45°πr}{180°}$=$\frac{1}{4}$πr,
故答案为:$\frac{1}{4}πr$.
点评 本题主要考查了扇形的面积,勾股定理,求出OD=$\frac{\sqrt{2}}{2}r$时△OCD的面积最大,∠COA=45°是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x$≥\frac{3}{2}$ | B. | x$≤\frac{3}{2}$ | C. | x$≥\frac{2}{3}$ | D. | x$≤\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
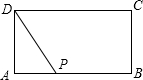 如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )
如图,在矩形ABCD中,AB=2a,AD=a,矩形边上一动点P沿A→B→C→D的路径移动.设点P经过的路径长为x,PD2=y,则下列能大致反映y与x的函数关系的图象是( )| A. | 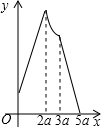 | B. | 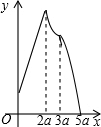 | C. | 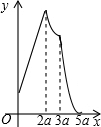 | D. | 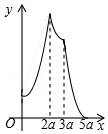 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
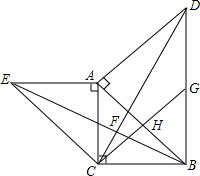 如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲 | 6.7 | 6 | 3.41 | 90% | 20% |
| 乙 | 7.1 | 7.5 | 1.69 | 80% | 10% |
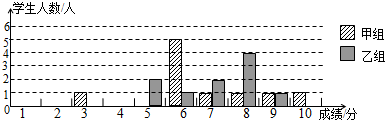
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
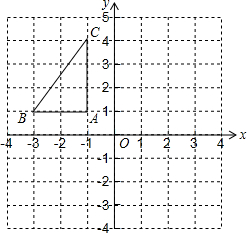 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com