解:(1)∵y=x-15,
y=0时,0=x-15,
∴x=15,
当x=0时,y=-15,
∴A(15,0),B(0,-15),
代入得
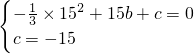
,
解得
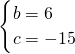
,
∴抛物线的解析式:y=-

x
2+6x-15.
(2)抛物线的解析式可变形为
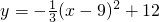
,
∴顶点D坐标为(9,12),
设y=0,则
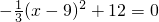
,
∴(x-9)
2=36.
∴x
1=3,x
2=15,
∴点C的坐标为(3,0),
∴
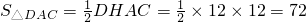
.
(3)∵点E是线段AD的中点,点H是线段AC的中点,.
∴点G是△DAC的重心.如图:
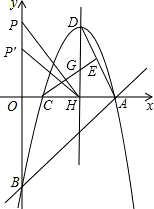
∵顶点D坐标为(9,12),
∴
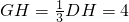
,
∴HO=9,CH=6.
设△POH∽△GHC时,
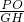
=
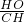
,
∴
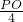
=
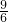
∴PO=6,
∴P
1(0,6);
△POH∽△CHG时,
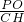
=
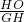
,
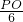
=

,
∴
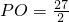
.
∴
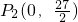
.
∴△POH能够与△CHG相似,相似时点P的坐标为P
1(0,6)或
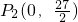
.
分析:(1)分别把x=0和y-0代入一次函数的解析式,求出A、B的坐标,代入抛物线得出方程组,求出方程组的解,即可得出抛物线的解析式;
(2)求出顶点D的坐标和C的坐标,根据三角形的面积公式求出即可;
(3)求出GH、HO、CH的值,根据相似三角形的性质得出两个比例式,代入即可求出P的坐标.
点评:本题考查了三角形的面积,用待定系数法求二次函数的解析式,二次函数图象上点的坐标,相似三角形的性质和判定等知识点的运用,主要培养了学生综合运用性质进行推理和计算的能力,题目比较典型,但有一定的难度,注意:分类讨论思想的运用.

 已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线
已知:如图,直线y=x-15与x轴、y轴分别相交于点A和点B.抛物线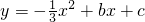 经过A、B两点.
经过A、B两点.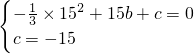 ,
,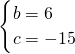 ,
, x2+6x-15.
x2+6x-15.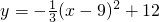 ,
,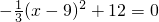 ,
,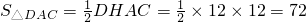 .
.
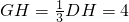 ,
,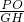 =
=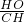 ,
,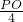 =
=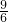
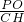 =
=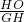 ,
,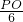 =
= ,
,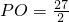 .
.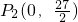 .
.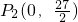 .
.

 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=