
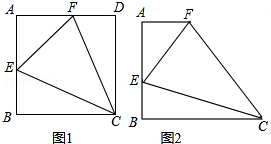
 如图1,在正方形ABCD中,∠ECF的两边分别交边AB、AD于点E、F,且∠ECF=45°.
如图1,在正方形ABCD中,∠ECF的两边分别交边AB、AD于点E、F,且∠ECF=45°.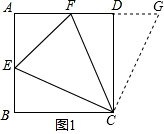
|
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图,已知∠AOB=∠COD=90°,OB平分∠DOE,下列说法:
如图,已知∠AOB=∠COD=90°,OB平分∠DOE,下列说法:| 1 |
| 2 |
| A、①② | B、①③ |
| C、①②③ | D、①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
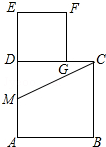 如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )
如图,在边长为2的正方形ABCD中,M为边AD的中点,延长MD至点E,使ME=MC,以DE为边作正方形DEFG,点G在边CD上,则DG的长为( )A、
| ||
B、3-
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
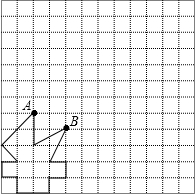 为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:
为迎接2014年8月16号在南京举行的青奥会,江都体育迷小强利用网格设计了一个“火炬”图案,请你帮帮他:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.
如图,在△ABC中,AD是BC边上的高,将△ABD沿AD折叠得到△AED,点E落在CD上,∠B=50°,∠C=30°.查看答案和解析>>
科目:初中数学 来源: 题型:
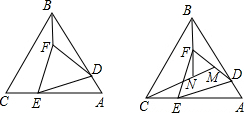 如图,等边△ABC中,D、E分别在AB、AC边上,且CE=2AD,将线段DE绕点D顺时针旋转60°得到线段DF,连接EF、BF;
如图,等边△ABC中,D、E分别在AB、AC边上,且CE=2AD,将线段DE绕点D顺时针旋转60°得到线段DF,连接EF、BF;| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com