
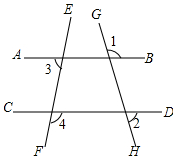
 如图,已知直线AB、CD与直线EF、GH相交,且∠1+∠2=180°,∠3=70°,求∠4的度数.
如图,已知直线AB、CD与直线EF、GH相交,且∠1+∠2=180°,∠3=70°,求∠4的度数. 科目:初中数学 来源: 题型:选择题
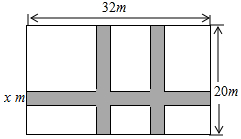 如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )
如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2.若设道路的宽为xm,则下面所列方程正确的是( )| A. | (32-2x)(20-x)=570 | B. | 32x+2×20x=32×20-570 | ||
| C. | (32-x)(20-x)=32×20-570 | D. | 32x+2×20x-2x2=570 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
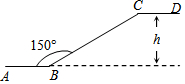 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )| A. | 4$\sqrt{3}$m | B. | 8m | C. | $\frac{8}{3}$$\sqrt{3}$m | D. | 4m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一节课上,数学老师在黑板上给出了这样一道题目:
一节课上,数学老师在黑板上给出了这样一道题目:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
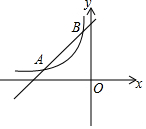 如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.
如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
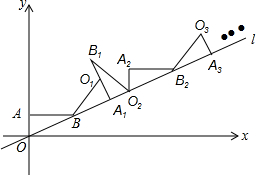 如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.
如图,直线l经过平面直角坐标系的原点O,且与x轴正方向的夹角是30°,点A的坐标是(0,1),点B在直线l上,且AB∥x轴,则点B的坐标是($\sqrt{3}$,1),现将△ABO绕点B顺时针旋转到△A1BO1的位置,使点A的对应点A1落在直线l上,再将△A1BO1绕点A1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线l上,顺次旋转下去…,则点A6的横坐标是$\frac{9}{2}$+$\frac{9}{2}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
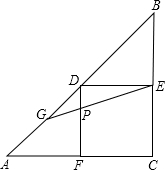
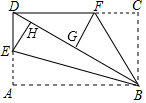 如图,将边长分别为6,2$\sqrt{3}$的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是①②(只填序号)
如图,将边长分别为6,2$\sqrt{3}$的矩形硬纸片ABCD折叠,使AB,CB均落在对角线BD上,点A与点H重合,点C与点G重合,折痕分别为BE,BF.下面三个结论:①∠EBF=45°;②FG是BD的垂直平分线;③DF=5.其中正确的结论是①②(只填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com