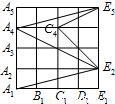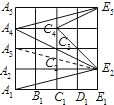
解:连接A
3E
2.
∵A
3A
2=A
1A
2,A
2E
2=A
2E
2,∠A
3A
2E
2=∠A
1A
2E
2=90°,
∴Rt△A
3A
2E
2≌Rt△A
1A
2E
2(SAS).
∴∠A
3E
2A
2=∠A
1E
2A
2.
由勾股定理,得
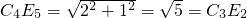
,

,
∵A
4C
4=A
3C
3=2,
∴△A
4C
4E
5≌△A
3C
3E
2(SSS).
∴∠A
3E
2C
3=∠A
4E
5C
4.
∴∠A
1E
2A
2+∠A
4E
2C
4+∠A
4E
5C
4=∠A
3E
2C
4+∠A
4E
2C
4+∠A
3E
2C
3=∠A
2E
2C
4.
由图可知△E
2C
2C
4为等腰直角三角形.
∴∠A
2E
2C
4=45度.
即∠A
1E
2A
2+∠A
4E
2C
4+∠A
4E
5C
4=45°.
分析:要求∠A
1E
2A
2+∠A
4E
2C
4+∠A
4E
5C
4的度数,不能把其中每个角度数求出,只能把这几个角的和转换成等于一个已知角.所以连接A
3E
2,容易证明Rt
△A3A2E2≌Rt
△A1A2E2,得到∠A
3E
2A
2=∠A
1E
2A
2.再通过利用勾股定理计算证明可以得到△A
4C
4E
5≌△A
3C
3E
2,这样∠A
3E
2C
3=∠A
4E
5C
4,再利用图形的已知条件进行转换可以得到:∠A
1E
2A
2+∠A
4E
2C
4+∠A
4E
5C
4=∠A
2E
2C
4=45°.
点评:此题要多次应用全等三角形的判定与性质,把题目要求的几个角之和转换到等于一个知道具体度数的角.

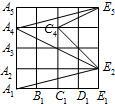 如图,正方形网格的每一个小正方形的边长都是1,试求∠A1E2A2+∠A4E2C4+∠A4E5C4的度数.
如图,正方形网格的每一个小正方形的边长都是1,试求∠A1E2A2+∠A4E2C4+∠A4E5C4的度数. 解:连接A3E2.
解:连接A3E2.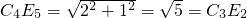 ,
, ,
,