
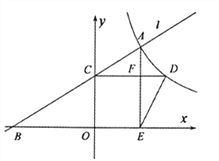
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
【答案】(1)(![]() a,
a,![]() );(2)y=
);(2)y=![]() x+3.
x+3.
【解析】
(1)由A点坐标可表示出AE的长,利用相似三角形的性质可求得CO的长,代入反比例函数解析式可表示出D点坐标;
(2)由条件可求得D点坐标,由平行四边形的性质可得△ACF∽△ABE,利用相似三角形的性质可求得a的值,则可求得A点坐标,由A、C的坐标,利用待定系数法可求得直线l的函数表达式.
(1)∵点A的横坐标是a,∴点A的纵坐标为![]() ,∴AE=
,∴AE=![]() ,
,
∵AE⊥x轴,∴CO∥AE,∴△BOC∽△BEA,∴![]() =
=![]() =
=![]() ,∴CO=
,∴CO=![]() ,
,
把y=![]() 代入y=
代入y=![]() ,解得x=
,解得x=![]() a,∴D点坐标为(
a,∴D点坐标为(![]() a,
a,![]() );
);
(2)∵OC=3,∴D点纵坐标为3,把y=3代入y=![]() 可得x=4,∴D(4,3),∴CD=4,
可得x=4,∴D(4,3),∴CD=4,
∵四边形BCDE是平行四边形,∴BE=CD=4,且CD∥BE,∴△ACF∽△ABE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得a=2,∴A(2,6),且C(0,3),
,解得a=2,∴A(2,6),且C(0,3),
∴可设直线l的函数表达式为y=kx+3,把x=2,y=6代入,可得6=2k+3,解得k=![]() ,
,
∴直线l的函数表达式为y=![]() x+3.
x+3.


科目:初中数学 来源: 题型:
【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2 ![]() ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 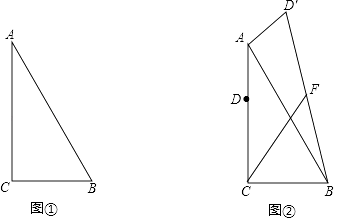
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图像如图所示,抛物线的对称轴为直线x=﹣1,P1(x1 , y1),P2(x2 , y2)是抛物线上的点,P3(x3 , y3)是直线l上的点,且x3<﹣1<x1<x2 , 则y1 , y2 , y3的大小关系是( ) 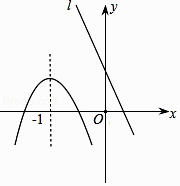
A.y1<y2<y3
B.y2<y3<y1
C.y3<y1<y2
D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC. 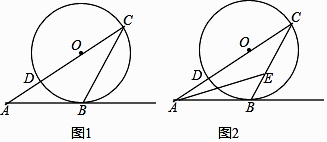
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个老太太提着一个篮子去卖鸡蛋,第一个人买走了她的鸡蛋的一半又半个;第二个人买走了剩下的一半又半个;第三人买走了前两个人剩下的一半又半个,正好卖完全部鸡蛋,问老太太一共卖了多少个鸡蛋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完一元一次方程解法,数学老师出了一道解方程题目:
![]() .李铭同学的解题步骤如下:
.李铭同学的解题步骤如下:
解:去分母,得3(x+1)-2(2-3x)=1;……①
去括号,得3x+3-4-6x=1; ……②
移项,得3x-6x=1-3+4; ……③
合并同类项,得-3x=2; ……④
系数化为1,得x=-![]() . ……⑤
. ……⑤
(1)聪明的你知道李铭的解答过程在第_________(填序号)出现了错误,出现上面错误的原因是违背了____.(填序号)①去括号法则;②等式的性质1;③等式的性质2;④加法交换律.
(2)请你写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将边长为2的正方形OABC如图①放置,O为原点. (Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.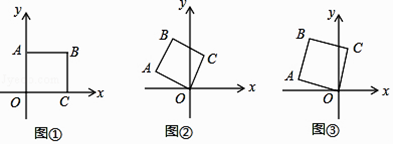
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划租一间商铺,下面是某房屋中介提供的两种商铺的出租信息:

设租期为x(月),所需租金为y(元),其中x为大于1的整数.
(1)若小王计划租用的商铺为90m2,请分别写出在商座A,B租商铺所需租金yA(元),yB(元)与租期x(月)之间的函数关系式;
(2)在(1)的前提下,请你帮助小王根据租期,租用哪个商座的商铺房租更低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.a2+a3=a5
B.(﹣2a2)3÷( ![]() )2=﹣16a4
)2=﹣16a4
C.3a﹣1= ![]()
D.(2 ![]() a2﹣
a2﹣ ![]() a)2÷3a2=4a2﹣4a+1
a)2÷3a2=4a2﹣4a+1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com