
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC. 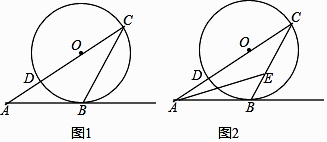
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.
【答案】
(1)解:连接OB,如图1,
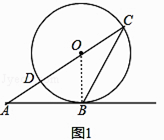
∵AB切⊙O于B,
∴∠ABO=90°,
∵∠A=26°,
∴∠AOB=90°﹣26°=64°,
∵OC=OB,
∴∠C=∠CBO,
∵∠AOB=∠C+∠CBO,
∴∠C= ![]() =32°
=32°
(2)解:连接OB,如图2,
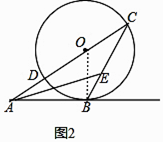
∵AE平分∠BAC,
∴∠CAE= ![]() ∠CAB,
∠CAB,
∵由(1)知:∠OBE=90°,∠C=∠CBO,
又∵∠C+∠CAB+∠CBA=180°,
∴2∠C+2∠CAE=90°,
∴∠CAE+∠C=45°,
∴∠AEB=∠CAE+∠C=45°
【解析】(1)连接OB,根据切线性质求出∠ABO=90°,根据三角形内角和定理求出∠AOB,求出∠C=∠OBC,根据三角形外角性质求出即可;(2)根据三角形内角和定理求出2∠C+2∠CAE=90°,求出∠C+∠CAE=45°,根据三角形外角性质求出即可.
【考点精析】认真审题,首先需要了解三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角),还要掌握三角形的外角(三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】育才中学组织七年级师生去春游,如果单租45座客车若干辆,则刚好坐满;如果单租60座的客车,则少租一辆,且余15个座位.
(1)求参加春游的师生总人数.
(2)已知一辆45座客车的租金每天250元,一辆60座客车的租金每天300元,问单租哪种客车省钱?
(3)如果同时租用这两种客车,那么两种客车分别租多少辆最省钱?(只写出租车方案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答 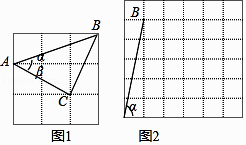
(1)如图1,如果ɑ,β都为锐角,且tanɑ= ![]() ,tanβ=
,tanβ= ![]() ,则ɑ+β=;
,则ɑ+β=;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ= ![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON , 使得∠MON=ɑ﹣β.此时ɑ﹣β=度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
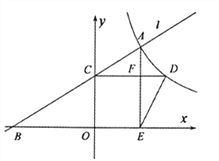
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 的图像上的一个动点,经过点
的图像上的一个动点,经过点![]() 的直线
的直线![]() 交
交![]() 轴负半轴于点
轴负半轴于点![]() ,交
,交![]() 轴正半轴于点
轴正半轴于点![]() .过点
.过点![]() 作
作![]() 轴的垂线,交反比例函数的图像于点
轴的垂线,交反比例函数的图像于点![]() .过点
.过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .设点
.设点![]() 的横坐标是
的横坐标是![]() .
.
(1)若![]() ,求点
,求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值,并求出此时直线
的值,并求出此时直线![]() 对应的函数表达式.
对应的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0
(1)求点C表示的数:
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动
(i)当P、Q两点在数轴上D点相遇时,求此时C、D两点之间的距离;
(ii),若AP+BQ=2PQ,求时间t.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com