
【题目】下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,第![]() 个图案中白色正方形的个数比黑色的正方形个数多______个.(用含
个图案中白色正方形的个数比黑色的正方形个数多______个.(用含![]() 的代数式表示)
的代数式表示)

【答案】4n+3
【解析】
通过观察图形很容易可知黑色正方形个数与图形的序号是相同的,即第n个图中黑色正方形的个数是n;而白色正方形的个数是所有正方形的个数总和减去黑色正方形的个数即3+6n-n所以白色正方形的个数-黑色正方形的个数=(3+6n-n)-n=3+4n.
由图可知
第1个图中:黑色正方形的个数是:1;白色正方形的个数是:3+6-1=3+6![]() 1-1;
1-1;
第2个图中:黑色正方形的个数是:2;白色正方形的个数是:3+6+6-2=3+6![]() 6-2;
6-2;
第3个图中:黑色正方形的个数是:3;白色正方形的个数是:3+6+6+6-3=3+6![]() 3-3;
3-3;
…
第n个图中:黑色正方形的个数是:n;白色正方形的个数是:3+6n-n;
所以第n个图案中白色正方形的个数比黑色的正方形个数多(3+6n-n)-n=3+4n.
故答案为: 4n+3;


科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:千克) |
|
|
|
|
|
|
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20筐白菜中,最重的一筐比最轻的一筐重______千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价![]() 元,则出售这20筐白菜可卖多少元?
元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在RtABC中,∠ACB=90°,BAC=30°,BC=6. (I)如图①,将线段CA绕点C顺时针旋转30°,所得到与AB交于点M,则CM的长=;
(II)如图②,点D是边AC上一点D且AD=2 ![]() ,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 .
,将线段AD绕点A旋转,得线段AD′,点F始终为BD′的中点,则将线段AD绕点A逆时针旋转度时,线段CF的长最大,最大值为 . 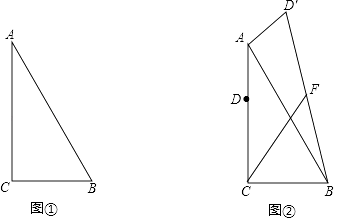
查看答案和解析>>
科目:初中数学 来源: 题型:
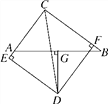
【题目】如图,在△ABC中,AC=6,BC=8,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
(1)求证:AE=BF;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费” 两部分组成.为了鼓励市民节约用水,其中城市供水费按阶梯式计费:一个月用水10吨以内(包括10吨)的用户,每吨收1.5元;一个月用水超过10吨的用户,10吨水仍按每吨1.5元收费,超过10吨的部分,按每吨2元收费.另外污水处理费按每吨0.65元收取.
(1)某居民5月份用水8吨,应交水费多少元? 6月份用水12吨,应交水费多少元?
(2)若某户某月用水x吨,请你用含有x的代数式表示该月应交的水费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线和直线l在同一直角坐标系中的图像如图所示,抛物线的对称轴为直线x=﹣1,P1(x1 , y1),P2(x2 , y2)是抛物线上的点,P3(x3 , y3)是直线l上的点,且x3<﹣1<x1<x2 , 则y1 , y2 , y3的大小关系是( ) 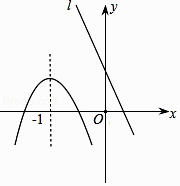
A.y1<y2<y3
B.y2<y3<y1
C.y3<y1<y2
D.y2<y1<y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC. 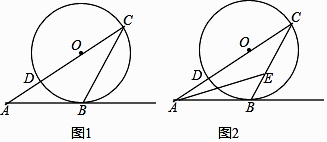
(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划租一间商铺,下面是某房屋中介提供的两种商铺的出租信息:

设租期为x(月),所需租金为y(元),其中x为大于1的整数.
(1)若小王计划租用的商铺为90m2,请分别写出在商座A,B租商铺所需租金yA(元),yB(元)与租期x(月)之间的函数关系式;
(2)在(1)的前提下,请你帮助小王根据租期,租用哪个商座的商铺房租更低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com