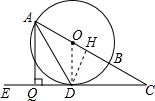
解:(1)连接OD,
∵∠ADE=∠DAC+∠C,
又∠ADE=60°,∠C=30°,
∴∠DAC=30°,
∵OD=OA,
∴∠DAC=∠ODA=30°,
又∠ADE=60°,
∴∠ODE=∠ODA+∠ADE=30°+60°=90°,
即OD⊥DC,
∴CD是⊙O的切线;
(2)作DH⊥AC于H,
∵AQ⊥EC,
∴∠AQD=90°,
∴∠QAD=30°,
由(1)得:∠DAC=30°,
∴∠QAD=∠DAC,即DA平分∠QAC,
又∵AQ⊥EC,
∴DH=DQ,
在Rt△AQD中,设DQ=x,则AD=2x,于是10
2+x
2=4x
2,
解得x=
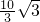
,
即点D到AC的距离为

.
分析:(1)连接OD,根据三角形外角的性质可得∠ADE=∠DAC+∠C,易求∠DAC=30°,而OD=OA,可得∠DAC=∠ODA=30°,从而可求∠ODE=90°,易证CD是⊙O的切线;
(2)作DH⊥AC于H,根据(1)可知∠DAC=30°,而易求∠QAD=30°,易知AD是∠QAC的角平分线,而D再角平分线上,故DH=DQ,在Rt△AQD中,利用30°的角所对的边等于斜边的一半,结合勾股定理易求DQ,从而可求DH.
点评:本题考查了切线的判定、角平分线的性质、勾股定理、等腰三角形的性质,解题的关键是利用三角形外角性质求出∠DAC=30°.

 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°. 解:(1)连接OD,
解:(1)连接OD,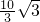 ,
, .
.
