
分析 (1)设骑电动车速度为xkm/h,则开车的平均速度为3xkm/h,根据等量关系:小王开车到单位比他骑电动车到单位少用20分钟可得出方程,解出即可;
(2)计算出骑电动车、开车及回家取手机的时间和,然后与30比较即可作出判断.
解答 解:设骑电动车速度为xkm/h,则开车的平均速度为3xkm/h,可得:$\frac{10}{x}-\frac{10}{3x}=\frac{20}{60}$,
解得:x=20,
经检验x=20是原分式方程的解,且符合题意,
答:小王骑电动车的平均速度20km/h;
(2)小王回家的时间:$\frac{5}{20}=\frac{1}{4}$小时,开车到单位的时间:$\frac{10}{20×3}=\frac{1}{6}$小时,共用时间:$(\frac{1}{4}+\frac{1}{6})×60+4=29$分钟,因为29<30,
所以小王能按时上班.
点评 此题考查了分式方程的应用,设出骑电动车速度的速度,根据等量关系得出方程是解答本题的关键,注意分式方程一定要检验.


科目:初中数学 来源: 题型:解答题
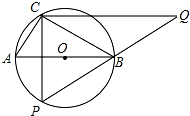 如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.
如图,Rt△ABC中,AB=10,AC:BC=3:4,以斜边AB为直径作⊙O,动点P在直径下方的半圆AB上运动(不与A、B重合),过点C作CQ⊥CP,与PB的延长线交于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{700}{x}$=$\frac{500}{x+10}$ | B. | $\frac{700}{x-10}$=$\frac{500}{x}$ | C. | $\frac{700}{x}$=$\frac{500}{x-10}$ | D. | $\frac{700}{x+10}$=$\frac{500}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 38 | B. | 34 | C. | 28 | D. | 44 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com