Question

如图，已知A(－4，0)，B(0，4)，现以A点为位似中心，相似比为9∶4，将OB向右侧放大，B点的对应点为C．

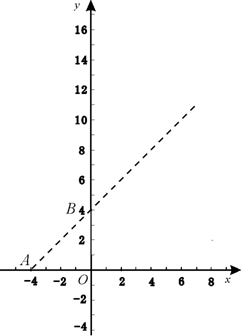
(1)求C点坐标及直线BC的解析式；

(2)一抛物线经过B、C两点，且顶点落在x轴正半轴上，求该抛物线的解析式并画出函数图象；

(3)现将直线BC绕B点旋转与抛物线相交与另一点P，请找出抛物线上所有满足到直线AB距离为的点P．

解：

Answer 1

答案：
解析：

解：(1)过C点向x轴作垂线，垂足为D，由位似图形性质可知： 　　△ABO∽△ACD，∴． 　　由已知，可知：． 　　∴．∴C点坐标为．　2分 　　直线BC的解析是为： 　　化简得：　3分 　　(2)设抛物线解析式为，由题意得：， 　　解得：　 　　∴解得抛物线解析式为或． 　　又∵的顶点在x轴负半轴上，不合题意，故舍去． 　　∴满足条件的抛物线解析式为　5分 　　(准确画出函数图象)　7分 　　(3)将直线BC绕B点旋转与抛物线相交与另一点P，设P到直线AB的距离为h，故P点应在与直线AB平行，且相距的上下两条平行直线和上．　8分 　　由平行线的性质可得：两条平行直线与y轴的交点到直线BC的距离也为． 　　如图，设与y轴交于E点，过E作EF⊥BC于F点， 　　在Rt△BEF中，， 　　∴．∴可以求得直线与y轴交点坐标为　10分 　　同理可求得直线与y轴交点坐标为　11分 　　∴两直线解析式；． 　　根据题意列出方程组：(1)；(2) 　　∴解得：；；； 　　∴满足条件的点P有四个，它们分别是，，，　15分 　　[注：对于以上各大题的不同解法，解答正确可参照评分！]