
【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案: 方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
【答案】解:方案一可获利润:140×1000=140000(元); 方案二可获利润:4500×140=630000(元);
方案三可获利润:15×6×7500+(140﹣15×6)×1000=725000(元);
方案四:设精加工x吨食蔬菜,则粗加工(140﹣x)吨蔬菜,
根据题意得: ![]() +
+ ![]() =15,
=15,
解得:x=60,
∴140﹣x=80.
此情况下利润为:60×7500+80×4500=810000(元),
∵140000<630000<725000<810000,
∴企业选择方案四所获利润最多
【解析】根据总利润=单吨利润×销售质量即可求出方案一、二、三的利润,在方案四种,设精加工x吨食蔬菜,则粗加工(140﹣x)吨蔬菜,根据每天可精加工6吨或粗加工16吨结合加工总天数为15天即可得出关于x的一元一次方程,解之即可得出x的值,进而得出140﹣x的值,再根据总利润=精加工部分的利润+粗加工部分的利润求出方案四的利润,将四种方案获得的利润比较后即可得出结论.


科目:初中数学 来源: 题型:
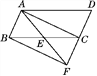
【题目】如图,已知点E是ABCD中BC边的中点,连接AE并延长交DC的延长线于点F.
(1)连接AC,BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形;
(2)在(1)的条件下,若△AFD是等边三角形,且边长为4,求四边形ABFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
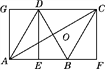
【题目】如图,在矩形AFCG中,BD垂直平分对角线AC,交CG于D,交AF于B,交AC于O.连接AD,BC.
(1)求证:四边形ABCD是菱形;
(2)若E为AB的中点,DE⊥AB,求∠BDC的度数;
(3)在(2)的条件下,若AB=1,求菱形ABCD的对角线AC,BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列4个命题:①对顶角相等;②同位角相等;③在同一个圆中,同一条弦所对的圆周角都相等;④圆的内接四边形对角互补.其中,真命题为( )
A. ①②④B. ①③④C. ①④D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com