
���� ��1������D��DE��BC������ΪE����֤���ı���ABED�Ǿ��Σ�Ȼ����Rt��DEC�У���������������Ǻ���ֵ���DE��EC�ij����Ӷ������AB��AD�ij���
��2�����ɡ�BPF�ס�DMF���õ���BPF=��DMF=90�㣬�Ӷ���֪����P��F��M��һ��ֱ���ϣ�
����ͼ3��ͼ4��ʾ�������tan��DBE=2��Ȼ��ֱ��ʾ��PF��MN�ij���Ȼ����������ε������ʽ�г�����x�ķ��̣������t��ֵ���Ӷ�����õ�P��λ�ã�
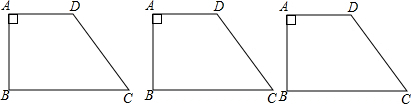
��� �⣺��1������D��DE��BC������ΪE��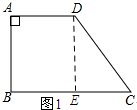
��AD��BC��
���ABC=��BAD=90�㣮
��DE��BC��
���DEB=90�㣮
���ABC=��BAD=��DEB=90�㣮
���ı���ABED�Ǿ��Σ�
��AB=DE��AD=BE��
����Rt��DEC�У���C=45�㣬CD=8$\sqrt{2}$��
��EC=DE=DC•sin45��=8$\sqrt{2}��\frac{\sqrt{2}}{2}$=8��
��AB=DE=8��AD=EB=BC-EC=12-8=4��
��2������ͼ2��ʾ��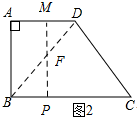
�ߡ�BPF�ס�DMF��
���BPF=��DMF=90�㣮
��PF��AD��
���P��F��M��һ��ֱ���ϣ�
���˶�ʱ��Ϊt��ʱ����BPF�ס�DMF����BP=t��DM=t��
��DM=PE��
��4-t=t��
��ã�t=2��
����ͼ3��ʾ������D��DE��BC������ΪE��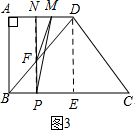
�ɣ�1����֪��DE=8��BE=4��
��tan��DBE=$\frac{DE}{BE}$=2��
��PF=2BP=2t��
MN=AD-AN-MD=4-t-t=4-2t��
��$\frac{1}{2}��2t����4-2t��$=2��
��ã�t=1��
��BP=1��
��ͼ4��ʾ������D��DE��BC������ΪE��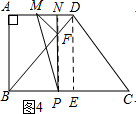
�ɣ�1����֪��DE=8��BE=4��
��tan��DBE=$\frac{DE}{BE}$=2��
��PF=2BP=2t��
MN=AN+MD-AD=2t-4��
��$\frac{1}{2}��2t����2t-4��$=2��
��ã�${t}_{1}=1-\sqrt{2}$����ȥ����t2=1$+\sqrt{2}$��
��PB=1$+\sqrt{2}$��
������������BP=1��BP=1$+\sqrt{2}$ʱ����PFM�����Ϊ2cm2��
���� ������Ҫ�������������Ǻ����Ķ��塢���ε����ʡ����������ε����ʡ������ε������ʽ����һԪ���η��̵�Ӧ�ã��������⻭�����������ͼ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
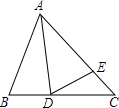 ��֪����ͼ���ȱߡ�ABC�У�D��E�ֱ���BC��AC�ϵĵ㣬�ҡ�ADE=60��
��֪����ͼ���ȱߡ�ABC�У�D��E�ֱ���BC��AC�ϵĵ㣬�ҡ�ADE=60���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
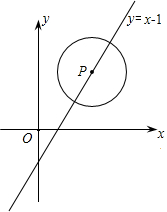 ��ͼ����֪��P�İ뾶Ϊ1��Բ��P��ֱ��y=x-1��ͼ�����˶�������P��x������ʱ����P�������Ϊ��2��1����0��-1����
��ͼ����֪��P�İ뾶Ϊ1��Բ��P��ֱ��y=x-1��ͼ�����˶�������P��x������ʱ����P�������Ϊ��2��1����0��-1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
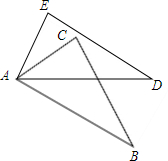 ��ͼ��ʾ��AB=AD��AC=AE��BC=DE�������EAD=70�㣬��CAD=40�㣬���BAD�Ķ�����
��ͼ��ʾ��AB=AD��AC=AE��BC=DE�������EAD=70�㣬��CAD=40�㣬���BAD�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | k��0 | B�� | k��0 | C�� | k��0 | D�� | k��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com