
����Ŀ����ͼ����������A���ʾ��a��B���ʾ��b��AB��ʾA���B��֮��ľ�������a��b����![]() ��
��
��1����A��B����֮��ľ�����
��2�����������ϴ���һ��C����AC=2BC����C���ʾ������
��3������ԭ��O����һ������һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶����������������������Ĵ�С���ɿ���һ������ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt��������
�ٷֱ��ʾ�ס�����С��ԭ��ľ�������t��ʾ����
����ס�����С��ԭ��ľ������ʱ������ʱ����
![]()
���𰸡���1��8����2��c=![]() ��c=14����3��t=
��c=14����3��t=![]() ���t=8�룮
���t=8�룮
�������������������1���ȸ��ݷǸ������������a��b��ֵ���ٸ��������ľ��빫ʽ�������A��B����֮��ľ��룻��2����C�����߶�AB�Ϻ��߶�AB���ӳ���������������ۼ�����⣻��3���ټ���ԭ��ľ���=�����˶���·��+OA�ij�������ԭ��ľ�����������������0��t��3ʱ������ӵ�B����ʼ�����˶���һֱ��ԭ��O����ʱOB�ij���-�����˶���·�̼�Ϊ����ԭ��ľ��룻����t��3ʱ�������ԭ��O����ʼ�����˶�����ʱ�����˶���·��-OB�ij��ȼ�Ϊ����ԭ��ľ��룻�ڷ��������������0��t��3������t��3�����ݼס�����С��ԭ��ľ�������г�����t�ķ��̣��ⷽ�̼��ɣ�
���������
��1����![]() ����a+2=0��b+3a=0����a=2��b=6��
����a+2=0��b+3a=0����a=2��b=6��
��AB�ľ���=|ba|=8��
��2���������ϵ�C��ʾ����Ϊc��
��AC=2BC����|ca|=2|cb|����|c+2|=2|c6|��
��AC=2BC��BC�����C��������BA���ӳ����ϣ���C��������߶�AB�Ϻ��߶�AB���ӳ����ϣ�
�ٵ�C�����߶�AB��ʱ������2��c��6����c+2=2��6c�������c=![]() ��
��
�ڵ�C�����߶�AB���ӳ�����ʱ������c��6����c+2=2��c6�������c=14��
�ʵ�AC=2BCʱ��c=![]() ��c=14��
��c=14��
��3���١����˶���·��Ϊ��1t=t��OA=2���������ԭ��ľ���Ϊ��t+2��
����ԭ��ľ�������������
����0��t��3ʱ������ӵ�B����ʼ�����˶���һֱ��ԭ��O����OB=6�������˶���·��Ϊ��2t=2t��������ԭ��ľ���Ϊ��62t��
����t��3ʱ�������ԭ��O����ʼһֱ�����˶�����ʱ����ԭ��ľ���Ϊ��2t6��
�ڵ�0��t��3ʱ����t+2=62t�����t=![]() ��
��
��t��3ʱ����t+2=2t6�����t=8��
�ʵ�t=![]() ���t=8��ʱ��������С��ԭ��ľ�����ȣ�
���t=8��ʱ��������С��ԭ��ľ�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���ֱ��y=2x��1����ƽ�ƶ�4����λ���Ⱥ�����ֱ�ߵĽ���ʽΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
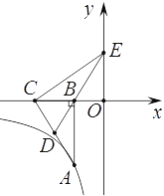
����Ŀ����ͼ����֪��A�ڷ���������![]() �ϣ���Rt��ABC����DΪб��AC���е㣬��DB���ӳ���y���ڵ�E������BCE�����Ϊ8��
�ϣ���Rt��ABC����DΪб��AC���е㣬��DB���ӳ���y���ڵ�E������BCE�����Ϊ8��
��1����֤����EOB�ס�ABC��
��2�����������Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ƚǵ�����������д���������������ô����������ʽ ____________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|a|=8��|b|=5����a��0��b��0��a��b��ֵ�ǣ� ��
A.3
B.��3
C.13
D.��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ���˽���꼶ѧ������������������һ����ѧ������һ�����������ԣ������Գɼ���������������ͳ��ͼ����ͬѧ������ڶ����Ƶ����0.08����ͬѧ������������ҵ�һ���������������Ƶ����Ϊ2��4��17��15�����ͳ��ͼ�ش��������⣺
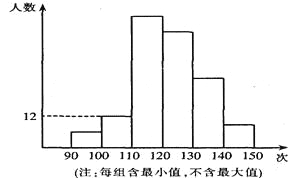
(1)��ι�����˶�����?
(2)����������������130��Ϊ���㣬����β��Գɼ����������Ƕ���?
(3)����У���꼶��600��ѧ��������Ƹ�У���꼶�ﵽ����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����,��1+2-1+2-2+��+2-2 016��ֵ.
��:��S=1+2-1+2-2+��+2-2016, ��
��2S=2+1+2-1+��+2-2 015, ��
��-����S=2-2-2 016.
����´˼���:
(1)1+3-1+3-2+��+3-2 016;
(2)1+3-1+3-2+��+3-n(n������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,A,O,B��ͬһ��ֱ����,��AOD=��BOD=��EOC=90��,��BOC�á�AOE=3��1.
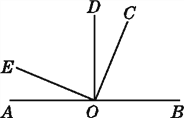
(1)���COD�Ķ���.
(2)ͼ�����ļ��Խǻ�Ϊ���?
(3)ͼ�����ļ��Խǻ�Ϊ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ʵ���õ����ݱ������߶�ÿ����1km�����´�Լ�½�3�棬��֪�õص����¶�Ϊ21�森
��1���߿�ij���߶���6km����˴����¶��Ƕ��٣�
��2���߿�ij���¶�Ϊ��24�棬��˴��ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com