
 如图,D为△ABC的边AB上的点,请补充一个条件
如图,D为△ABC的边AB上的点,请补充一个条件科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,连接BE,且∠BED=60°,若CE=5,△ACD的面积为| 35 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
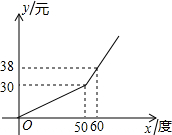 电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电
电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电查看答案和解析>>
科目:初中数学 来源: 题型:
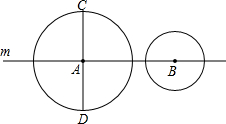 如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是
如图,⊙A的直径为8,⊙B的直径为6,A、B两点均在直线m上,且⊙A的直径CD与直线m垂直,当点B在直线m上移动时,设AB=d,若⊙B运动到和⊙A、CD都有交点时,d的取值范围是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com