
如图所示,小华在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离EB=20米,镜子与小华的距离ED=2米,此时小华刚好从镜子中看到铁塔顶端A.已知小华的眼睛距地面的高度CD=1.5米,则铁塔AB的高度是( )

A.15米 B.16米 C.17米 D.18米
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:2015年人教版初中数学九年级27本章检测卷(解析版) 题型:解答题
(2014上海)已知:如图,梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD相交于点F,点E是边BC延长线上一点,且∠CDE=∠ABD.
(1)求证:四边形ACED是平行四边形;
(2)连接AE,交BD于点G.求证: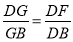 .
.

查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.3练习卷(解析版) 题型:解答题
在平面直角坐标系中,五边形ABCDE的五个顶点分别为A(-2,3),B(-4,2),C(-3,0),D(-1,1),E(-1,2),以坐标原点为位似中心,将五边形ABCDE放大,使放大后的五边形的边长是原五边形对应边长的2倍,比较放大后的图形,你能得到什么结论?
查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.3练习卷(解析版) 题型:解答题
如图所示,学校操场上有一旗杆AB,甲在操场上的C处直立一根3米高的竹竿CD,甲从C处退后3米到达E处,恰好看到竹竿的顶端D与旗杆的顶端B重合,甲的眼睛到地面的距离FE为1.5米,身高相同的乙在C1处也直立一根3米高的竹竿C1D1,乙从C1处退后4米到达E1处,恰好看到竹竿的顶端D1与旗杆的顶端B也重合(点A,C,E,C1,E1在同一条直线上),量得EE1=6米,求旗杆AB的高.

查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.3练习卷(解析版) 题型:填空题
(2014贵州遵义)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,已知矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=________里.

查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.3练习卷(解析版) 题型:解答题
一位同学想利用树的影长测量树高,他在某一时刻测得长为1m的竹竿的影长为0.9m,但当他马上测量树的影长时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子落在墙上,如图,他先测得留在墙上的影子高CD为1.2m,又测得地面上的影子长BC为2.7m,则树高AB为多少?

查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.2练习卷(解析版) 题型:解答题
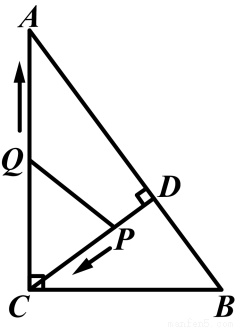
(2014黑龙江牡丹江)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位,当点P运动到C时,两点都停止,设运动时间为t秒.
(1)求线段CD的长.
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ︰S△ABC=9︰100?若存在,求出t的值;若不存在,说明理由.
(3)当t为何值时,△CPQ为等腰三角形?
查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.2练习卷(解析版) 题型:选择题
(2014江苏南京)若△ABC∽△A′B′C′,相似比为1︰2,则△ABC与△A′B′C′的面积的比为( )
A.1︰2 B.2︰1 C.1︰4 D.4︰1
查看答案和解析>>
科目:初中数学 来源:2015年人教版初中数学九年级27.2.1练习卷(解析版) 题型:解答题
如图,△ADE∽△ABC,∠AED=∠C,分别找出△ADE的各边的对应边和各角的对应角,并写出对应边的比例式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com