
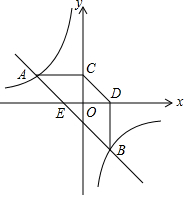
 如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.
如图,已知A(-4,n),B(4-n,-4)是直线y=kx+b和双曲线y=$\frac{m}{x}$的两个交点,过点A,B分别作AC⊥y轴,BD⊥x轴,垂足为C,D.分析 (1)根据反比例函数图象上点的坐标特征得出m=-4n=(4-n)•(-4),解得n=2,m=-8,得出双曲线的解析式,把A、B点坐标代入直线解析式根据待定系数法,可求得直线解析式;
(2)不等式的解析集即为直线在双曲线上方时对应的x的范围,结合图象可求得其解集.
(3)分别求得OC=2,OD=2,△COD是等腰直角三角形,得出∠ODC=45°,由直线的斜率可知∠DEB=45°,证得∠ODC=∠DEB,即可证得CD∥AB.
解答 解:(1)∵A(-4,n),B(4-n,-4)在双曲线y=$\frac{m}{x}$上,
∴m=-4n=(4-n)•(-4),
解得n=2,m=-8,
∴A(-4,2),B(2,-4),
代入y=kx+b得:$\left\{\begin{array}{l}{-4k+b=2}\\{2k+b=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=-2}\end{array}\right.$,
∴直线解析式为y=-x-2,双曲线的解析式为y=-$\frac{8}{x}$;
(2)∵等式kx+b-$\frac{m}{x}$≥0的解集即为直线在双曲线上方对应的x的取值范围,
∴不等式的解集为x≤-4或0<x≤2.
(3)∵A(-4,2),B(2,-4),
∴OC=2,OD=2,
∴OC=OD,
∴∠ODC=45°,
由直线y=-x-2可知∠DEB=45°,
∴∠ODC=∠DEB,
∴CD∥AB.
点评 本题主要考查一次函数与反比例函数的交点,掌握两函数图象的交点坐标满足两函数解析式是解题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:初中数学 来源: 题型:填空题
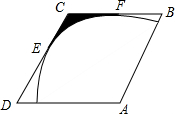 如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.
如图,菱形ABCD的边长为2,∠A=120°,以点A为圆心的圆弧与菱形ABCD的DC,BC两边相切,切点分别为点E、F,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
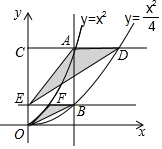 如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )
如图,垂直于x轴的直线AB分别与抛物线C1:y=x2(x≥0)和抛物线C2:y=$\frac{{x}^{2}}{4}$(x≥0)交于A,B两点,过点A作CD∥x轴分别与y轴和抛物线C2交于点C,D,过点B作EF∥x轴分别与y轴和抛物线C1交于点E,F,则$\frac{{S}_{△OFB}}{{S}_{△EAD}}$的值为( )| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k>-$\frac{2}{3}$ | B. | k>$\frac{2}{3}$ | C. | k≤$\frac{2}{3}$ | D. | k≥-$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
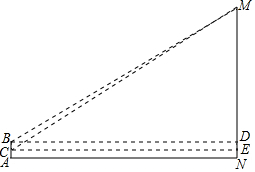 某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)
某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.
如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com