
解:(1)∵点A(1,1)在反比例函数
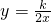
的图象上,
∴k=2.
∴反比例函数的解析式为:

.
一次函数的解析式为:y=2x+b.
∵点A(1,1)在一次函数y=2x+b的图象上,∴b=-1.
∴一次函数的解析式为:y=2x-1;
(2)∵点A(1,1)
∴∠AOB=45°.
∵△AOB是直角三角形
∴点B只能在x轴正半轴上.
①当∠OB
1A=90°时,即B
1A⊥OB
1.
∵∠AOB
1=45°,∴B
1A=OB
1,∴B
1(1,0).
②当∠OAB
2=90°时,∠AOB
2=∠AB
2O=45°,
∴B
1是OB
2中点,∴B
2(2,0).
综上可知,B点坐标为(1,0)或(2,0).
分析:(1)只需把交点的坐标分别代入解析式,即可求得待定系数的值;
(2)此题注意要就直角的问题进行分情况讨论.
点评:此题的难点是第(2)小题,当没有明确说明直角时,要注意能够分情况讨论.

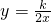 的图象交于点A(1,1)
的图象交于点A(1,1) 解:(1)∵点A(1,1)在反比例函数
解:(1)∵点A(1,1)在反比例函数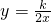 的图象上,
的图象上, .
.
