
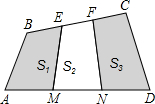
 如图所示,在四边形ABCD中,AM=MN=ND,BE=EF=FC,四边形ABEM,MEFN,NFCD的面积分别记为S1,S2和S3,求
如图所示,在四边形ABCD中,AM=MN=ND,BE=EF=FC,四边形ABEM,MEFN,NFCD的面积分别记为S1,S2和S3,求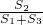 =?
=?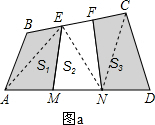 解:如图a所示:连接AE、EN和NC,设四边形AECN的面积为S,
解:如图a所示:连接AE、EN和NC,设四边形AECN的面积为S, S,S△AEM+S△CNF=
S,S△AEM+S△CNF= S.
S. S△AEC,S△CDN=
S△AEC,S△CDN= S△CNA,
S△CNA,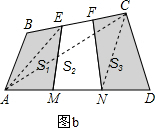 上面两个式子相加得S△ABE+S△CDN=
上面两个式子相加得S△ABE+S△CDN= ×四边形AECN的面积=
×四边形AECN的面积= S,
S, S+
S+ S=S,
S=S,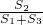 =
=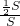 =
= .
.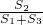 =
= .
.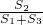 即可.
即可.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com