
【题目】如图,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点开始以每秒1个单位的速度匀速沿
点开始以每秒1个单位的速度匀速沿![]() 轴向左移动.
轴向左移动.

(1)点![]() 的坐标:________;点
的坐标:________;点![]() 的坐标:________;
的坐标:________;
(2)求![]() 的面积
的面积![]() 与
与![]() 的移动时间
的移动时间![]() 之间的函数解析式;
之间的函数解析式;
(3)在![]() 轴右边,当
轴右边,当![]() 为何值时,
为何值时,![]() ,求出此时点
,求出此时点![]() 的坐标;
的坐标;
(4)在(3)的条件下,若点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,
,![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,求点
处,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]()
【解析】
(1)在![]() 中,分别令y=0和x=0,则可求得A、B的坐标;
中,分别令y=0和x=0,则可求得A、B的坐标;
(2)利用t可表示出OM,则可表示出S,注意分M在y轴右侧和左侧两种情况;
(3)由全等三角形的性质可得OM=OB=2,则可求得M点的坐标; .
(4)由勾股定理可得:![]() ,折叠可知;
,折叠可知;![]() ,可得:
,可得:![]() ,故
,故![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,在
,在![]() 中,根据勾股定理可列得方程
中,根据勾股定理可列得方程![]() ,即可求出答案.
,即可求出答案.
解:(1)在![]() 中, 令y=0可求得x=4, 令x=0可求得y=2,
中, 令y=0可求得x=4, 令x=0可求得y=2,
∴A(4,0),B(0,2)
故答案为:(4,0) ;(0,2)
(2)由题题意可知AM=t,
①当点M在y轴右边时,OM=OA-AM=4-t,
∵N (0,4)
∴ON=4,
∴![]() ,
,
即![]() ;
;
当点![]() 在
在![]() 轴左边时,则OM=AM-OA=t-4,
轴左边时,则OM=AM-OA=t-4,
∴![]() ,
,
即![]() .
.
∴![]()
(3)若![]() ,则有
,则有![]() ,
,
∴![]() .
.
(4)由(3)得,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 沿
沿![]() 折叠后与
折叠后与![]() 重合,
重合,
∴![]() ,
,
∴![]() ,
,
∴此时点![]() 在
在![]() 轴的负半轴上,
轴的负半轴上,![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
解得![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).

(1)图2中的阴影部分的面积为 ;
(2)观察图2请你写出(a+b)2、(ab)2、ab之间的等量关系是 ;
(3)根据(2)中的结论,若m+n=5,mn=4,则mn= ;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图①,当点D在边BC上时,且n等于30°,则∠BAD= ,∠CDE= ;
(2)如图②,当点D运动到点B左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由;
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请在图③中画出图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点D,下列结论:①△BCD是等腰三角形;②BD是∠ABC的平分线;③DC+BC=AB;④△AMD≌△BCD,正确的是 ( )

A.①②B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
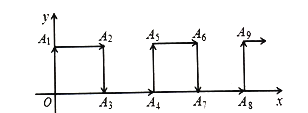
【题目】如图,在平面直角坐标系中,一动点从原点![]() 出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点
出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点![]() ,
,![]() ,
,![]() ,
,![]() ,...那么点
,...那么点![]() 的坐标为( ).
的坐标为( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
(1)1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)有46.4吨货物需要运输,货运公司拟安排大小货车共10辆(要求两种货车都要用),全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com