
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少? .
.
【答案】
(1)解:当1≤x<50时,y=(200﹣2x)(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(200﹣2x)(90﹣30)=﹣120x+12000
(2)解:当1≤x<50时,二次函数开口向下,二次函数对称轴为x=45,
当x=45时,y最大=﹣2×452+180×45+2000=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
【解析】(1)根据单价乘以数量,可得利润,可得答案.
(2)根据分段函数的性质,可分别得出最大值,根据比较可得答案.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,其对称轴为直线x=﹣1,给出下列结果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
则正确的结论是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.
(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线与直线的图象如图所示,当y1≠y2时,取y1 , y2中的较大值记为N;当y1=y2时,N=y1=y2 . 则下列说法: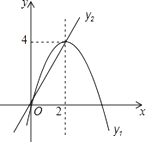
①当0<x<2时,N=y1;
②N随x的增大而增大的取值范围是x<0;
③取y1 , y2中的较小值记为M,则使得M大于4的x值不存在;
④若N=2,则x=2﹣ ![]() 或x=1.
或x=1.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x﹣1=0,②![]() x+1=0,③x﹣(3x+1)=﹣5中,不等式组
x+1=0,③x﹣(3x+1)=﹣5中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组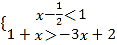 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程3﹣x=2x,3+x=2(x+![]() )都是关于x的不等式组
)都是关于x的不等式组![]() 的关联方程,直接写出m的取值范围.
的关联方程,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示玲玲骑自行车离家的距离与时间的关系.她9点离开家,15点回到家,请根据图象回答下列问题:

(1)玲玲到达离家最远的地方是什么时间?她离家多远?
(2)她何时开始第一次休息?休息了多长时间?
(3)第一次休息时,她离家多远?
(4)11点~12点她骑车前进了多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com