
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )
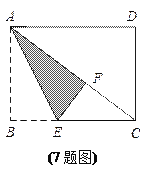
A. 3 B. 4
C. 5 D. 6
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于C点,且A(﹣2,0)、B(4,0),其顶点为D,连接BD,点P是线段BD上的一个动点(不与B、D重合),过点P作y轴的垂线,垂足为E,连接BE.
(1)求抛物线的解析式,并写出顶点D的坐标;
(2)设P点的坐标为(x,y),△PBE的面积为S,求S与x之间的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取值最大值时,过点P作x轴的垂线,垂足为F,连接EF,△PEF沿直线EF折叠,点P的对应点为点P′,请直接写出P′点的坐标,并判断点P′是否在该抛物线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有人.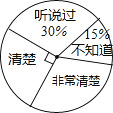
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.
(1)求证:△ABD∽△AEB;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)在(2)的条件下,作∠BAC的平分线,与BE交于点F,若AF=2,求⊙C的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中考考生最喜欢做哪种类型的英语客观题,2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查,要求每位考生都自主选择其中一个类型,为此随机调查了各考点部分考生的意向.并将调查结果绘制成如图的统计图表(问卷回收率为100%,并均为有效问卷).
被调查考生选择意向统计表
题型 | 所占百分比 |
听力部分 | a |
单项选择 | 35% |
完型填空 | b |
阅读理解 | 10% |
口语应用 | c |
根据统计图表中的信息,解答下列问题:
(1)求本次被调查的考生总人数及a、b、c的值;
(2)将条形统计图补充完整;
(3)全市参加这次中考的考生共有42000人,试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点.
(1)如图1,当点P在线段AB上(不与A、B两点重合)运动时,∠1、∠2、∠3之间有怎样的大小关系?请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠1、∠2、∠3之间的大小关系为________;
(3)如图3,当点P在线段BA的延长线上运动时,∠1、∠2、∠3之间的大小关系为________.
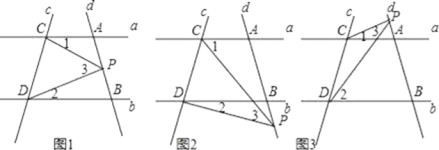
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com