
分析 (1)根据判别式为0时,一元二次方程有两个相等的实数根解答即可;
(2)把方程组用代入法化为一元二次方程,根据根的判别式进行解答.
解答 解:(1)由题意得,△=4+4k=0,
解得k=-1,
则方程为x2-2x+1=0,
解得x1=x2=1;
(2)$\left\{\begin{array}{l}{x-y-k=0①}\\{{x}^{2}-2y-1=0②}\end{array}\right.$,
由①得,y=x-k③,
把③代入②,
x2-2x+2k-1=0,
△=4-8k+4=0,
解得k=1,
∴当k=1时,关于x、y的方程组$\left\{\begin{array}{l}x-y-k=0\\{x^2}-2y-1=0\end{array}\right.$只有一组实数解.
点评 本题考查的是高次方程的解法和一元二次方程根的判别式的应用,掌握当判别式为0时,一元二次方程有两个相等的实数根是解题的关键.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
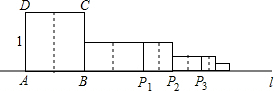 如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.
如图,正方形ABCD的边长为1,AB边与直线l重合,沿AB边的中垂线将正方形剪开,剪开后的右侧部分以B为中心,顺时针旋转90°,得到以BP1为边的新矩形,我们称之为第1次操作;沿BP1边的中垂线将矩形剪开,再将剪开后的右侧部分以点P1为中心,顺时针旋转90°,得到以P1P2为边的正方形,我们称之为第2次操作…按此规律继续操作下去,AP2016的长为AP2016=$\frac{{2}^{1010}-3}{{2}^{1008}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
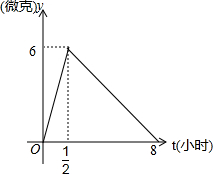 某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?
某医药研究所开发一种新药,如果承认按规定的剂量服用,据监测,服药后每毫升血液中含药量y与时间t之间关系如图所示,据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为6:00,那么服药后几点到几点有效?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
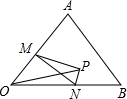 如图,在△AOB内有一定点P,OP=3,∠AOB=45°,点M,N分别为AO,BO上的点,那么△PMN的周长的最小值是3$\sqrt{2}$,此时,∠MPN的度数是90°.
如图,在△AOB内有一定点P,OP=3,∠AOB=45°,点M,N分别为AO,BO上的点,那么△PMN的周长的最小值是3$\sqrt{2}$,此时,∠MPN的度数是90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
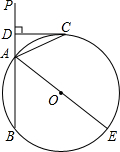 如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,
如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com