
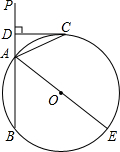
 如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,
如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,分析 (1)连结OC,如图,根据切线的性质得OC⊥CD,则有OC∥BP,根据平行线的性质得∠1=∠2,加上∠2=∠3,则∠1=∠3,所以AC平分∠PAE;
(2)作OH⊥AB于H,如图,根据垂径定理得到AH=BH=$\frac{1}{2}$AB=4,设⊙O的半径为r,由四边形OHDC为矩形得到DH=OC=r,OH=CD,则DA=r-4,CD=10-r,所以OH=10-r,然后在Rt△OAH中利用勾股定理得到∴42+(10-r)2=r2,再解方程求出r即可.
解答 (1)证明: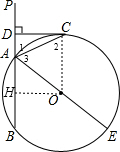 连结OC,如图,
连结OC,如图,
∵CD是⊙O的切线,
∴OC⊥CD,
∵BP⊥CD,
∴OC∥BP,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴AC平分∠PAE;
(2)解:作OH⊥AB于H,如图,则AH=BH=$\frac{1}{2}$AB=4,
设⊙O的半径为r,易得四边形OHDC为矩形,
∴DH=OC=r,OH=CD,
∴DA=r-4,
而AD+CD=6,
∴CD=6-(r-4)=10-r,
∴OH=10-r,
在Rt△OAH中,∵AH2+OH2=OA2,
∴42+(10-r)2=r2,解得r=$\frac{29}{5}$,
即⊙O的半径为$\frac{29}{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理和勾股定理.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
| 每天售出的T恤件数 | 160 | 140 | 120 |
| 频数 | 2 | 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解一批炮弹的杀伤半径 | |
| B. | 了解某市电视台《焦点》栏目的收视率 | |
| C. | 了解某班学生对“消防知识”的知晓率 | |
| D. | 了解某河域中鱼的种类 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com