
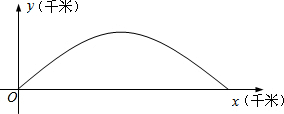
分析 (1)求炮的最大射程即求 y=kx-$\frac{1}{20}$(1+k2)x2(k>0)与x轴的横坐标,求出后应用基本不等式求解即可.
(2)求炮弹击中目标时的横坐标的最大值,由一元二次方程根的判别式求解即可.
解答 (1)解:根据题意得:$y=kx-\frac{1}{20}(1+{k^2}){x^2}=0$,
即:$x=\frac{20k}{{1+{k^2}}}=\frac{20}{{k+\frac{1}{k}}}$,
∵${(\sqrt{k}-\frac{1}{{\sqrt{k}}})^2}≥0$,
∴$k+\frac{1}{k}≥2$,
∴$x=\frac{20}{{k+\frac{1}{k}}}≤10$,
∴炮弹的最大射程是10千米.
(2)解:∵速度与炮弹的射程有关,炮弹能够击中目标.∴k>0,
根据题意的:$y=kx-\frac{1}{20}(1+{k^2}){x^2}=3.2$,
整理得:x2k2-20xk+64+x2=0,
由△=(-20x)2-4x2(64+x2)≥0得:x≤6,
此时:$k=\frac{{20x+\sqrt{{{(-20x)}^2}-4{x^2}({x^2}+64)}}}{{2{x^2}}}>0$(不考虑另一根)
∴飞行物的横坐标不超过6千米时,炮弹能够击中它.
点评 本题考查函数模型的运用,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
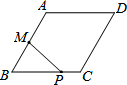 如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )| A. | 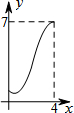 | B. | 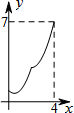 | C. | 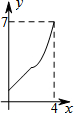 | D. | 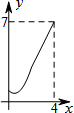 ? ? |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
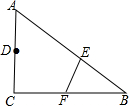 如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.
如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
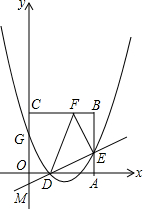 如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.
如图所示,正方形OABC的边长为2cm,以OA、OC所在直线为坐标轴建立直角坐标系xoy,点D、E、F和G分别从点O、A、B和C沿着OA、AB、BC和CO方向都以1cm/s的速度同时移动,移动时间为t(0<t<2)s,抛物线y=ax2+bx+c总是经过三个动点G、D、E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
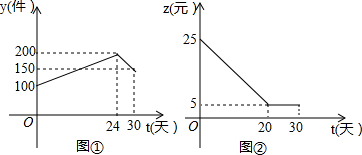
| A. | 第24天的销售量为200件 | |
| B. | 第10天销售一件产品的利润是15元 | |
| C. | 第12天与第30天这两天的日销售利润相等 | |
| D. | 第30天的日销售利润是750元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com