
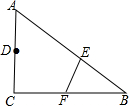
 如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$. 分析 连接DF、DE、DB,设BF为x,在Rt△CDF中,根据勾股定理求出x的值,再根据勾股定理求出BD的长,求出OF得到答案.
解答 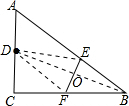 解:连接DF、DE、DB,
解:连接DF、DE、DB,
由题意得,DF=DB,OD=OB,
设BF为x,则DF为x,CF=9-x,
∵D是AC的中点,
∴CD=$\frac{1}{2}$AC=3,
在Rt△CDF中,
DF2=CD2+CF2,即x2=32+(9-x)2,
解得,x=5,
在Rt△CDB中,CD=3,BC=9,
则BD=3$\sqrt{10}$,
OD=$\frac{3}{2}\sqrt{10}$,
Rt△DOF中,OF=$\sqrt{D{F}^{2}-O{D}^{2}}$=$\frac{\sqrt{10}}{2}$,
∴EF=2OF=$\sqrt{10}$.
点评 本题考查的是翻折变换的性质,通过观察图形根据翻折的性质找出相等关系是解题的关键,解答时注意勾股定理的正确运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
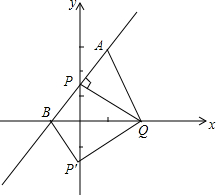 如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′
如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
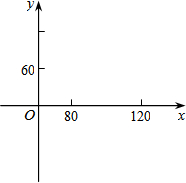 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上.
如图所示是一个等腰三角形纸片ABC,其中AB=AC,把∠B沿EM折叠,使点B落在点D上,把∠C沿FN折叠,使点C也落在点D上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则$\frac{EF}{GH}$的值是( )
如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则$\frac{EF}{GH}$的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 众数是35 | B. | 中位数是34 | C. | 平均数是35 | D. | 方差是6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com