
 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
分析 (1)根据表中的已知点的坐标利用待定系数法确定直线的解析式即可;
(2)根据总利润=单件利润×销量列出函数关系式配方后即可确定最值;
(3)令利润等于60求得相应的自变量的值即可确定销售单价的范围.
解答 解:(1)设y=kx+b,把(60,5),(80,4)代入得:$\left\{\begin{array}{l}{60k+b=5}\\{80k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{20}}\\{b=8}\end{array}\right.$,
故答案为:y=-$\frac{1}{20}$x+8;
(2)该公司年利润w=(-$\frac{1}{20}$x+8)(x-40)-100=-$\frac{1}{20}$(x-100)2+80,
当x=100时,该公司年利润最大值为80万元;
(3)由题意得:-$\frac{1}{20}$(x-100)2+80=60,
解得:x1=80,x2=120,
故该公司确定销售单价x的范围是:80≤x≤120.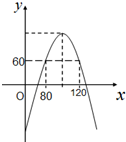
根据函数图象可得:当80≤x≤120时,
该公司产品的利润不低于60万元.
点评 本题考查了二次函数的应用,解题时把实际问题转化为二次函数,再对二次函数进行实际应用.此题为数学建模题,借助二次函数解决实际问题.


科目:初中数学 来源: 题型:解答题
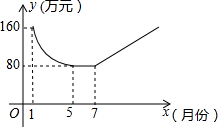 保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
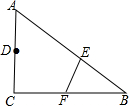 如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
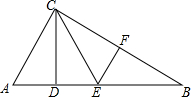 如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.
如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.
如图,一次函数y=-x+4的图象与反比例函数y=$\frac{k}{x}$(k为常数,且k≠0)的图象交于A(1,a),B两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20% | B. | 40% | C. | -220% | D. | 30% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com