
| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
分析 (1)商铺面积是x平方米时购买费用是(0.6x+1.2)万元、装修费用是0.3x2万元,根据总费用=购买费用+装修费用列出一元二次方程求解即可;
(2)①分40≤x≤58和58<x≤71时利用总利润=单件利润×销量列出有关的分段函数即可;
②分别求得利润的最大值,求差几块确定答案.
解答 解:(1)由条件:投资一个面积为x(单位:m2)的商铺,所需购买费用(单位:万元)与x+2成正比例,装修费用(单位:万元)与x2成正比例,和表格中的数据可得,商铺面积是x平方米时购买费用是(0.6x+1.2)万元、装修费用是0.3x2万元,
由题意列方程,0.3x2+0.6x+1.2=51.6
即(x+1)2=169,解得x1=12,x2=-14(舍去)
所以,小王投资的这个商铺的面积为12平方米;
(2)①当40≤x≤58时,w=(x-40)(-2x+140)=-2x2+220x-5600,
当58<x≤71时,w=(x-40)(-x+82)=-x2+122x-3280,
所以,w(元)与销售单价x(元/双)之间的函数关系式为:$w=\left\{\begin{array}{l}-2{x^2}+220x-5600(40≤x≤58)\\-{x^2}+122x-3280(58<x≤71)\end{array}\right.$,
②当40≤x≤58x=55
时,w=-2x2+220x-5600=-2(x-55)2+450
所以,当时,日最大销售利润为450元,月最大销售利润是13500元,
月最大盈余:13500-2075-3000=8420元,
当58<x≤71时,w=-x2+122x-3280=-(x-61)2+441,
当x=61时,日最大利润是441元,月最大销售利润是13230元,
月最大盈余:13230-2075-3000=8155元,
答:小王每月(按30天计算)能有盈余,最多盈余8420元.
点评 本题考查了二次函数综合知识,解题的关键是仔细审题,从复杂的题意中整理出二次函数模型,难度不大,重点是读懂题意.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
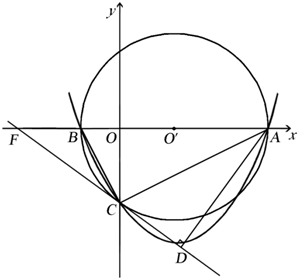 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:
一种产品的进价为40元,某公司在销售这种产品时,每年总开支为100万元(不含进价).经过若干年销售得知,年销售量y(万件)是销售单价x(元)的一次函数,并得到如下部分数据:| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 年销售量y(万件) | 5.5 | 5 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
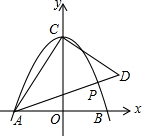 如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.
如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
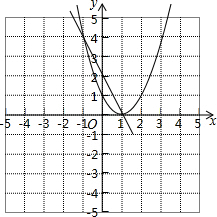 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com