
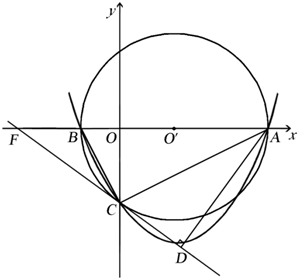
 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.分析 (1)根据自变量与函数值的对应关系,当y=0时,可得A、B点的坐标,当x=0时,可得C点坐标;
(2)根据切线与过切点直径的关系,可得CF的解析式,根据抛物线的顶点坐标公式,可得抛物线的顶点坐标,根据点的坐标是否满足函数解析式,可得答案;
(3)根据平行线间的距离相等,可得过O点平行AC的直线,及向下平移4个单位的直线,根据解方程组,可得符合条件的P点坐标.
解答 解:(1)当y=0时,$\frac{1}{4}$x2-$\frac{3}{2}$x-4=0,解得x1=-2,x2=8,
∵点B在点A的左侧,
∴点A的坐标为(-2,0),点B的坐标为(8,0).
当x=0时,y=-4,
∴点C的坐标为(0,-4);
(2)抛物线的顶点E是否在直线CD上,理由如下;
抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4的顶点坐标为(3,-$\frac{25}{4}$),
O′是AB的中点,得O′(3,0),
直线O′C的解析式为y=$\frac{4}{3}$x-4,
CF是⊙O′的切线,得
CF的解析式为y=-$\frac{3}{4}$x-4,
当x=3时,y=-$\frac{25}{4}$,
即E(3,-$\frac{25}{4}$)在直线CD上;
(3)在抛物线上存在一点P,使得S△ACP=S△ACO,
直线AC的解析式为y=$\frac{1}{2}$x-4,向上平移4个单位的直线过O点,向下平移4个单位的直线上的点到AC的距离与O到AC的距离相等,
过O点平行AC的直线y=$\frac{1}{2}$x,
①联立抛物线、过O点平行于AC的直线,得
$\left\{\begin{array}{l}{y=\frac{1}{2}x}\\{y=\frac{1}{4}{x}^{2}-\frac{3}{2}x-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-4-4\sqrt{2}}\\{{y}_{1}=-2-2\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-4+4\sqrt{2}}\\{{y}_{2}=-2+2\sqrt{2}}\end{array}\right.$,
P1(-4-4$\sqrt{2}$,-2-2$\sqrt{2}$),P2(-4+4$\sqrt{2}$,-2+2$\sqrt{2}$);
②联立向下平移4个单位的直线、抛物线,得
$\left\{\begin{array}{l}{y=\frac{1}{2}x-8}\\{y=\frac{1}{4}{x}^{2}-\frac{3}{2}x-4}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=4}\\{y=-6}\end{array}\right.$,
即P3(4,-6).
综上所述:P1(-4-4$\sqrt{2}$,-2-2$\sqrt{2}$),P2(-4+4$\sqrt{2}$,-2+2$\sqrt{2}$),P3(4,-6).
点评 本题考查了二次函数综合题,(1)利用了自变量与函数值的对应关系;(2)利用了切线与过切点直径的关系,抛物线的顶点坐标,点与直线的位置关系;(3)利用等底等高的三角形的面积相等,利用了平行线间的距离相等,解方程组,利用平行线间的距离相等得出平行AC的两条直线是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
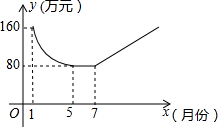 保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 商铺的面积(m2) | 购买费用(万元) | 装修费用(万元) |
| 1 | 1.8 | 0.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x2-1 | B. | y=x2+6x+5 | C. | y=x2+4x+4 | D. | y=x2+8x+17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com