
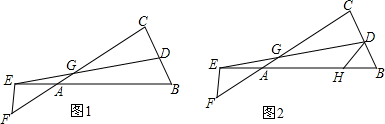
分析 (1)过E作EM⊥CF于M,证得△GEM∽△CGD,得到$\frac{DG}{EG}=\frac{DC}{EM}$,再由三角函数求得结果;
(2)在AH上截取AP=AF,过P作PQ⊥AC于Q,连接PD,得到△AEF≌△APQ,证出EF=PQ,由于EF=CD,等量代换PQ=CD,推出四边形PQCD是矩形,得到∠QPD=∠PDC=∠PDB=90°,得出∠1+∠2=∠3+∠4=90°,根据等腰三角形的性质得到PH=DH,于是得到结.
解答 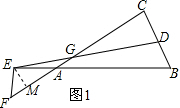 解:(1)过E作EM⊥CF于M,
解:(1)过E作EM⊥CF于M,
∵∠EGM=∠CGD,∠EMG=∠C,
∴△GEM∽△CGD,
∴$\frac{DG}{EG}=\frac{DC}{EM}$,
∵∠BAC=30°,
∴∠EAF=30°,
∴∠F=60°,
∴$\frac{CD}{EM}=\frac{EF}{EM}$=$\frac{1}{\frac{EM}{EF}}$=$\frac{1}{sin60°}$=$\frac{2\sqrt{3}}{3}$,
∴$\frac{DG}{EG}=\frac{2\sqrt{3}}{3}$;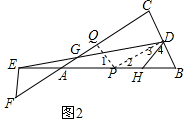
(2)在AH上截取AP=AF,过P作PQ⊥AC于Q,连接PD,
在△AEF与△APQ中,$\left\{\begin{array}{l}{∠EAF=∠QAP}\\{∠FEA=∠PQA}\\{AF=AP}\end{array}\right.$,
∴△AEF≌△APQ,
∴EF=PQ,
∵EF=CD,
∴PQ=CD,
∵∠PQC=∠C=90°,
∴PQ∥CD,
∴四边形PQCD是矩形,
∴∠QPD=∠PDC=∠PDB=90°,
∴∠1+∠2=∠3+∠4=90°,
∵HD=HB,
∴∠4=∠B,
∵∠1=∠B,
∴∠1=∠4,
∴∠2=∠3,
∴PH=DH,
∴AH=AP+PH=AF+DH.
点评 本题考查了相似三角形的判定和性质,锐角三角函数,等边三角形的判定和性质,作垂线构造相似三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
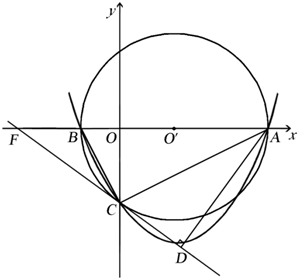 如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.
如图,抛物线y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4与x轴交于点A和点B(点B在点A的左侧),与轴交于点C,⊙O′是△ABC的外接圆,AB是⊙O′的直径,过点C作⊙O′的切线与x轴交于点F,过点A作AD⊥CF于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
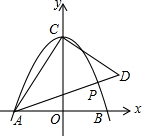 如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.
如图,抛物线y=ax2+4与x轴交于A、B两点(A在B的左边),与y轴交于点C,AB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(min) | 0 | 3 | 6 | 8 | 12 | … |
| y(m) | 5 | 70 | 5 | 54 | 5 | … |

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
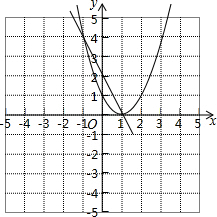 设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
设函数y=(x-1)[(k-1)x+(k-3)](k是常数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
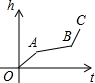 匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )
匀速地向一个容器内注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),这个容器的形状是下图中的( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
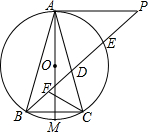 如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com