

分析 (1)作CH⊥AB于H,交DG于P,根据勾股定理求出AB,根据三角形的面积公式求出CH,根据相似三角形的性质计算即可;
(2)根据相似三角形的性质求出两个正方形的顶点分别在AC、BC上时,x的值即可;
(3)根据题意、结合图形,根据相似三角形的性质分别计算即可.
解答 解:(1)作CH⊥AB于H,交DG于P,
∵∠C=90°,AC=6,BC=8,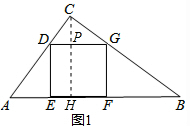
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∴CH=$\frac{\frac{1}{2}AC×BC}{\frac{1}{2}×AB}$=4.8,
∵四边形DEFG是正方形,
∴DG∥AB,
∴$\frac{DG}{AB}$=$\frac{CP}{CH}$,即$\frac{DG}{10}$=$\frac{4.8-DG}{4.8}$,
解得,DG=$\frac{120}{37}$,
故答案为:$\frac{120}{37}$;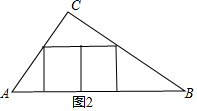
(2)如图2,当两个正方形的顶点分别在AC、BC上时,
设正方形的边长为x,
由(1)得,$\frac{2x}{10}$=$\frac{4.8-x}{4.8}$,
解得,x=$\frac{120}{49}$,
则小正方形边长x的范围是x≤$\frac{120}{49}$;
(3)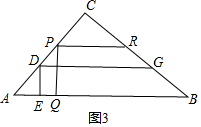 如图3,当DE=1时,
如图3,当DE=1时,
由(1)得,$\frac{DG}{10}$=$\frac{4.8-1}{4.8}$,
解得,DG=$\frac{95}{12}$,
则一条边都在AB上正方形的个数是7,
当PQ=2时,$\frac{PR}{10}$=$\frac{4.8-2}{4.8}$,
解得,PR=$\frac{35}{6}$,
则第二层正方形的个数是5,
同理,第三层正方形的个数是3,第④层正方形的个数是1,
则最多能摆放7+5+3+1=16个小正方形纸片.
故答案为:16.
点评 本题考查了正方形的性质和相似三角形的判定和性质,解题的关键是需要对正方形的性质、直角三角形的勾股定理和相似三角形的判定和性质熟练地掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
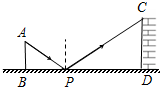 如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米.
如图,是小李设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.1米,BP=1.9米,PD=19米,那么该古城墙CD的高度是11米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.
如图,△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于D,E,BE=4CE,AD=$\sqrt{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com