已知:a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b).二次函数y=(x-2a)x-2b(x-a)+c2的图象的顶点在x轴上,且sinA、sinB是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两个根.
(1)判断△ABC的形状,关说明理由;
(2)求m的值;
(3)若这个三角形的外接圆面积为25π,求△ABC的内接正方形(四个顶点都在三角形三边上)的边长.
解:(1)△ABC是直角三角形,理由如下:
将y=(x-2a)x-2b(x-a)+c
2化简,整理得:y=x
2-2(a+b)x+2ab+c
2,
∵此函数图象的顶点在x轴上,
∴
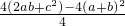
=0,
整理,得a
2+b
2=c
2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∴sinB=cosA,
∴sinA、cosA是关于x的方程(m+5)x
2-(2m-5)x+m-8=0的两个根,
∴
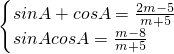
,
又∵sin
2A+cos
2A=1,
∴(sinA+cosA)
2-2sinA•cosA=1,
∴(
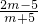
)
2-2×

=1,
整理,得m
2-24m+80=0,
解得m
1=20,m
2=4.
经检验,m
1=20,m
2=4都是原方程的根,
但是,当m
1=20时,sinA+cosA>0,sinA•cosA>0,
当m
2=4时,sinA+cosA>0,sinA•cosA<0,舍去,
∴m=20;
(3)∵△ABC的外接圆面积为25π,
∴外接圆半径R=5,
∴斜边c=10.
当m=20时,原方程变为25x
2-35x+12=0,
解得x
1=

,x
2=

,
∴a=8,b=6.
设正方形的边长为x.
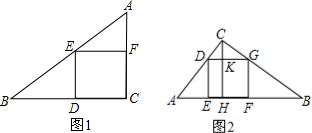
图1中,由EF:BC=AF:AC,得x:8=(6-x):6,
解得x=

;
图2中,CH=

,
CK:CH=DG:AB,(

-x):

=x:10,
解得x=
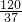
.
综上可知,△ABC的内接正方形(四个顶点都在三角形三边上)的边长为

或
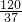
.
分析:(1)先由二次函数y=(x-2a)x-2b(x-a)+c
2的图象的顶点在x轴上,得到判别式△=0,进而得到a
2+b
2=c
2,再根据勾股定理的逆定理即可判定△ABC是直角三角形;
(2)先利用互余两角三角函数之间的关系得到sinB=cosA,再根据一元二次方程根与系数的关系得到
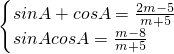
,然后利用同角三角函数之间的关系求得m的值;
(3)先由圆的面积公式求出△ABC的外接圆半径R=5,则斜边c=10,再将m=20代入方程(m+5)x
2-(2m-5)x+m-8=0,
得到25x
2-35x+12=0,解方程求出x的值,进而求得a=8,b=6.当正方形的四个顶点都在△ABC的三边上时,分两种情况进行讨论:①如图1,正方形CDEF有两条边在△ABC的直角边上;②如图2,正方形DEFG有一条边在△ABC的斜边上.
点评:本题考查了二次函数的性质,勾股定理的逆定理,互余两角、同角的三角函数之间的关系,一元二次方程根与系数的关系,相似三角形的判定与性质等知识,综合性较强,有一定难度.

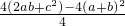 =0,
=0,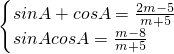 ,
,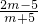 )2-2×
)2-2× =1,
=1, (3)∵△ABC的外接圆面积为25π,
(3)∵△ABC的外接圆面积为25π, ,x2=
,x2= ,
, ;
; ,
, -x):
-x): =x:10,
=x:10,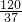 .
. 或
或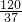 .
.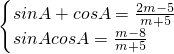 ,然后利用同角三角函数之间的关系求得m的值;
,然后利用同角三角函数之间的关系求得m的值;

 名校课堂系列答案
名校课堂系列答案 B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.
B两点的横坐标分别为1和2.过点B作BC垂直x轴于点C,△OBC的面积为2.