
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论: ①b2﹣4c>0;
②b+c+1=0;
③3b+c+6=0;
④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解:∵函数y=x2+bx+c与x轴无交点, ∴b2﹣4ac<0;
故①错误;
当x=1时,y=1+b+c=1,
故②错误;
∵当x=3时,y=9+3b+c=3,
∴3b+c+6=0;
③正确;
∵当1<x<3时,二次函数值小于一次函数值,
∴x2+bx+c<x,
∴x2+(b﹣1)x+c<0.
故④正确.
故选B
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】我们在学完“平移、轴对称、旋转”三种图形的变化后,可以进行进一步研究,请根据示例图形,完成下表.
图形的变化 | 示例图形 | 与对应线段有关的结论 | 与对应点有关的结论 |
平移 |
| AA′=BB′ | |
轴对称 |
| ||
旋转 |
| AB=A′B′;对应线段AB和A′B′所在的直线相交所成的角与旋转角相等或互补. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D均在以BC为直径的圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10,则图中阴影部分的面积为 . 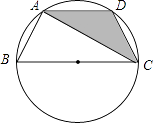
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每个月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定位多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2 , 四边形ABCD面积是11cm2 , 则①②③④四个平行四边形周长的总和为( ) 
A.48cm
B.36cm
C.24cm
D.18cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com