����⣺��1���ⷽ����
��
��ã�
��
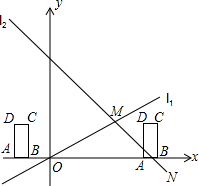
��M�������ǣ���4��2����
�ڽ���ʽy=-x+6�У���y=0����ã�x=6����N�������ǣ���6��0����
��2����0��t��1ʱ���غϲ�����һ�������Σ�OB=t�������
t���������
��t•
t=
t
2��
��1��t��4ʱ���غϲ�����ֱ�����Σ����εĸ���1���µ��ǣ�
t���ϵ��ǣ�
��t-1�����������ε������ʽ���Եõ���S=
[
t+
��t-1��]=
��t-
����
��4��t��5ʱ����M��x��Ĵ��ߣ����غϲ��ֱ����߷ֳ�����ֱ�����Σ��������ε��µ���2���ϵֱ��ǣ�-t+6��
��t-1�����������ε������ʽ�������
S=-
t
2+
t-
��
��5��t��6ʱ���غϲ�����ֱ�����Σ��뵱1��t��4ʱ���غϲ�����ֱ�����εļ��㷽����ͬ����S=
��13-2t����
��6��t��7ʱ���غϲ�����ֱ�������Σ����뵱0��t��1ʱ���ⷨ��ͬ���������S=
��7-t��
2��
��S=
| | t2(0��t��1) | | (t-)(1��t��4) | | -t2+t-(4��t��5) | | (13-2t)(5��t��6) | | (7-t)2(6��t��7) |
| |
��
��3����0��t��1ʱ������ֵy��t�������������t=1ʱ��ȡ�����ֵ�ǣ�
��
��1��t��4������ֵy��t�������������t=4ʱ��ȡ�����ֵ�ǣ�
��4-
��=
��
��4��t��5ʱ���Ƕ��κ������Գ���t=
�������ֵ�ǣ�-
����
��
2+
��
-
=
��
��5��t��6ʱ������ֵy��t���������С�������ֵ��
ͬ������6��t��7ʱ��y��t���������С�������ֵ��
��֮�����������ֵ�ǣ�
��

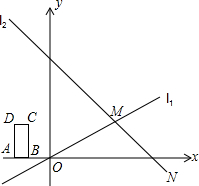 ֱ��l2��x���ཻ�ڵ�N��
ֱ��l2��x���ཻ�ڵ�N��



 ��2012•��Ǩ����ͼ��SO��SA�ֱ���Բ�ĸߺ�ĸ�ߣ���SA=12cm����ASO=30�㣬�����Բ�IJ������
��2012•��Ǩ����ͼ��SO��SA�ֱ���Բ�ĸߺ�ĸ�ߣ���SA=12cm����ASO=30�㣬�����Բ�IJ������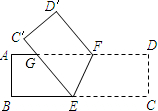 ��2012•��Ǩ����ͼ����һ�ž���ֽƬABCD��EF�۵���ʹ����C��D�ֱ����ڵ�C�䣬D�䴦��C��E��AF�ڵ�G������CEF=70�㣬���GFD��=
��2012•��Ǩ����ͼ����һ�ž���ֽƬABCD��EF�۵���ʹ����C��D�ֱ����ڵ�C�䣬D�䴦��C��E��AF�ڵ�G������CEF=70�㣬���GFD��=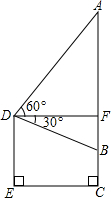 ��2012•��Ǩ����ͼ��ʹ�ò���Dz���һ���ڻ��߶ȵ�ʾ��ͼ����֪�ڻ�AB�ĵ˾������ĸ߶�BC=1m���ڱڻ�����ǰ����D����ñڻ��˵ĸ��ǡ�BDF=30�㣬�ҵ�D�������ĸ߶�DE=2m����ڻ�AB�ĸ߶ȣ�
��2012•��Ǩ����ͼ��ʹ�ò���Dz���һ���ڻ��߶ȵ�ʾ��ͼ����֪�ڻ�AB�ĵ˾������ĸ߶�BC=1m���ڱڻ�����ǰ����D����ñڻ��˵ĸ��ǡ�BDF=30�㣬�ҵ�D�������ĸ߶�DE=2m����ڻ�AB�ĸ߶ȣ�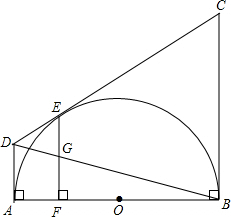 ��2012•��Ǩ����ͼ�����ı���ABCD�У���DAB=��ABC=90�㣬CD����ABΪֱ���İ�Բ�����ڵ�E��EF��AB�ڵ�F��EF��BD�ڵ�G����AD=a��BC=b��
��2012•��Ǩ����ͼ�����ı���ABCD�У���DAB=��ABC=90�㣬CD����ABΪֱ���İ�Բ�����ڵ�E��EF��AB�ڵ�F��EF��BD�ڵ�G����AD=a��BC=b��