
【题目】已知四边形ABCD中,AB=BC,∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD,DC(或它们的延长线)于E,F. 当∠MBN绕B点旋转到AE=CF时(如图1),易证AE+CF=EF;
当∠MBN绕B点旋转到AE≠CF时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE,CF,EF又有怎样的数量关系?请写出你的猜想,不需证明.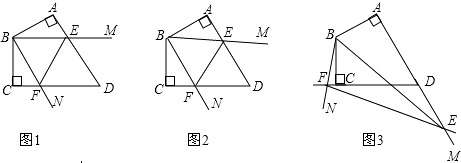
【答案】解:∵AB⊥AD,BC⊥CD,AB=BC,AE=CF, 在△ABE和△CBF中,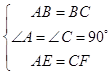 ,
,
∴△ABE≌△CBF(SAS);
∴∠ABE=∠CBF,BE=BF;
∵∠ABC=120°,∠MBN=60°,
∴∠ABE=∠CBF=30°,
∴AE= ![]() BE,CF=
BE,CF= ![]() BF;
BF;
∵∠MBN=60°,BE=BF,
∴△BEF为等边三角形;
∴AE+CF= ![]() BE+
BE+ ![]() BF=BE=EF;
BF=BE=EF;
图2成立,图3不成立.
证明图2.
延长DC至点K,使CK=AE,连接BK,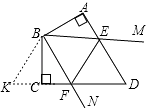
在△BAE和△BCK中,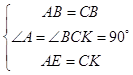
则△BAE≌△BCK,
∴BE=BK,∠ABE=∠KBC,
∵∠FBE=60°,∠ABC=120°,
∴∠FBC+∠ABE=60°,
∴∠FBC+∠KBC=60°,
∴∠KBF=∠FBE=60°,
在△KBF和△EBF中,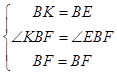
∴△KBF≌△EBF,
∴KF=EF,
∴KC+CF=EF,
即AE+CF=EF.
图3不成立,
AE、CF、EF的关系是AE﹣CF=EF.
【解析】根据已知可以利用SAS证明△ABE≌△CBF,从而得出对应角相等,对应边相等,从而得出∠ABE=∠CBF=30°,△BEF为等边三角形,利用等边三角形的性质及边与边之间的关系,即可推出AE+CF=EF. 同理图2可证明是成立的,图3不成立.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知点P在第二象限,并且到x轴的距离为1,到y轴的距离为2.则点P的坐标是( )
A. (1、2) B. (﹣1,2) C. (2,1) D. (﹣2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( ) 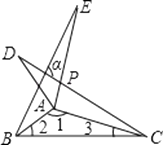
A.80°
B.100°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽像出的几何图形,B,C,E在同一条直线上,连结DC. 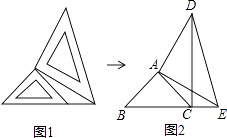
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的宇母);
(2)证明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“H”字,第一个“H”有7个棋子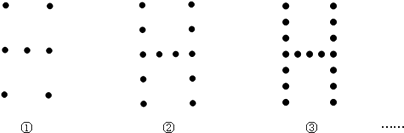
(1)摆成第二个“H”字需要几个棋子?第三个“H”字需要几个棋子?
(2)按这样的规律摆下去,摆成第10个“H”字需要几个棋子,第n个呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%,在销售中出现了滞销,于是先后两次降价,售价降为25元.
(1)求这种玩具的进价;
(2)求平均每次降价的百分率(精确到0.1%).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com