
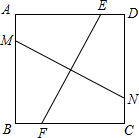
 已知,如图所示,正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MN.
已知,如图所示,正方形ABCD,E、M、F、N分别是AD、AB、BC、CD上的点,若EF⊥MN,求证:EF=MN. 证明:如图,过点E作EG⊥BC于G,过点M作MH⊥CD于H,
证明:如图,过点E作EG⊥BC于G,过点M作MH⊥CD于H,
|


科目:初中数学 来源: 题型:
| 3 | 4 |
 .5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?
.5个单位/秒的速度运动,问在整个运动的过程中,点P在动圆的园面(圆上和圆的内部)上一共运动了多长时间?查看答案和解析>>
科目:初中数学 来源: 题型:
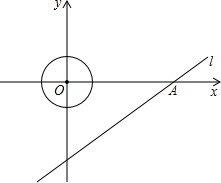
 已知:如图所示,直线l的解析式为y=
已知:如图所示,直线l的解析式为y=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市惠山六校联考九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知:如图所示,直线l的解析式为 ,并且与x轴、y轴分别交于点A、B.
,并且与x轴、y轴分别交于点A、B.

(1)求A、B两点的坐标;
(2)一个圆心在坐标原点、半径为1的圆,以0.4个单位/秒的速度向x轴正方向运动,问在什么时刻与直线l相切;
(3)在题(2)中,若在圆开始运动的同时,一动点P从B点出发,沿射线BA方向以0.5个单位/秒的速度运动,设t秒时点P到动圆圆心的距离为s,求s与t的关系式;
(4)问在整个运动过程中,点P在动圆的圆面(圆上和圆内部)上,一共运动了多长时间?
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省苏州市新区一中九年级(上)月考数学试卷(12月份)(解析版) 题型:解答题
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.
查看答案和解析>>
科目:初中数学 来源:《24.2 与圆有关的位置关系》2010年同步测试(解析版) 题型:解答题
 x-3,并且与x轴、y轴分别相交于点A、B.
x-3,并且与x轴、y轴分别相交于点A、B.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com